搜索
【题目】上午8时，一条船从海岛A出发，以15n mile/h（海里/时，1n mile＝1852m）的速度向正北航行，10时到达海岛B处，从A、B望灯塔C，测得NAC＝42°，NBC＝84°．则从海岛B到灯塔C的距离为（ ）
A.45n mileB.30n mileC.20n mileD.15n mile
参考答案：
【答案】B
【解析】
根据三角形外角的性质，求证∠C=∠NAC，然后即可证明BC=AB，从而求得B到C的距离．
∵∠NBC＝84°，∠NAC＝42°，
∴∠C＝84°﹣42°＝42°．
∴∠C＝∠NAC，
∴BC＝AB，
∵上午8时，一条船从海岛A出发，以15n mile/h的速度向正北航行．10时到达海岛B处，
∴BC＝AB＝15×2＝30n mile．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，
，
.点
从点
出发，沿折线
—
以每秒1个单位长度的速度向终点
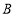运动，点
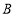从点出发沿折线
－
以每秒3个单位长度的速度向终点运动，、两点同时出发.分别过、两点作
于
，
于
.设点的运动时间为
（秒）.
（1）当
、两点相遇时，求的值.（2）在整个运动过程中，求
的长（用含的代数式表示）.（3）当
与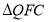
全等时，直接写出所有满足条件的
的长. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O且AB=AC，延长BC至点D，使CD=CA，连接AD交⊙O于点E，连接BE、CE．
（1）求证：△ABE≌△CDE；
（2）填空：
①当∠ABC的度数为 时，四边形AOCE是菱形；
②若AE=6，EF=4，DE的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
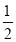BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) 
A. 90°B. 95°C. 100°D. 105°
-
科目： 来源： 题型：
查看答案和解析>>【题目】2018年5月12日是我国第十个全国防灾减灾日，也是汶川地震十周年．为了弘扬防灾减灾文化，普及防灾减灾知识和技能，郑州W中学通过学校安全教育平台号召全校学生进行学习，并对学生学习成果进行了随机抽取，现对部分学生成绩（x为整数，满分100分）进行统计．绘制了如图尚不完整的统计图表：
调查结果统计表
组别
分数段
频数
A
50≤x＜60
a
B
60≤x＜70
80
C
70≤x＜80
100
D
80≤x＜90
150
E
90≤x＜100
120
合计
b
根据以上信息解答下列问题：
（1）填空：a= ，b= ；
（2）扇形统计图中，m的值为 ，“D”所对应的圆心角的度数是 度；
（3）本次调查测试成绩的中位数落在 组内；
（4）若参加学习的同学共有2000人，请你估计成绩在90分及以上的同学大约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等边△ABC中，点D，E分别在边BC，AB上，且BD＝AE，AD与CE交于点F，作CM⊥AD，垂足为M，下列结论不正确的是（ ）
A. AD＝CE B. MF＝
CF C. ∠BEC＝∠CDA D. AM＝CM -
科目： 来源： 题型：
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度．如图6，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i=1：
．在离C点40米的D处，用测角仪测得大楼顶端A的仰角为37°，测角仪DE的高为1.5米，求大楼AB的高度约为多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
≈1.73．）
相关试题
