【题目】2018年5月12日是我国第十个全国防灾减灾日,也是汶川地震十周年.为了弘扬防灾减灾文化,普及防灾减灾知识和技能,郑州W中学通过学校安全教育平台号召全校学生进行学习,并对学生学习成果进行了随机抽取,现对部分学生成绩(x为整数,满分100分)进行统计.绘制了如图尚不完整的统计图表:
调查结果统计表
组别 | 分数段 | 频数 |
A | 50≤x<60 | a |
B | 60≤x<70 | 80 |
C | 70≤x<80 | 100 |
D | 80≤x<90 | 150 |
E | 90≤x<100 | 120 |
合计 | b |
根据以上信息解答下列问题:
(1)填空:a= ,b= ;
(2)扇形统计图中,m的值为 ,“D”所对应的圆心角的度数是 度;
(3)本次调查测试成绩的中位数落在 组内;
(4)若参加学习的同学共有2000人,请你估计成绩在90分及以上的同学大约有多少人?

参考答案:
【答案】(1)50、500;(2)30、108;(3)D(4)480人
【解析】
(1)由B组频数及其所占百分比可得总人数b的值,再根据各分组人数之和等于总人数可得a的值;
(2)用D组人数除以总人数可得m的值,用360°乘以D组人数所占百分比;
(3)根据中位数的定义求解可得;
(4)利用样本估计总体思想求解可得.
(1)∵被调查的总人数b=80÷16%=500人,
∴a=500﹣(80+100+150+120)=50,
故答案为:50、500;
(2)m%=![]() ×100%=30%,即m=30,
×100%=30%,即m=30,
“D”所对应的圆心角的度数是360°×![]() =108°,
=108°,
故答案为:30、108;
(3)本次调查测试成绩的中位数是第250、251个数据的平均数,而这2个数据均落在D组,
∴本次调查测试成绩的中位数落在D组,
故答案为:D.
(4)估计成绩在90分及以上的同学大约有2000×24%=480人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
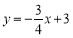 与
与 轴,
轴, 轴分别交于
轴分别交于 点和
点和 点,点
点,点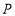 为
为 轴上的一个动点,若三角形
轴上的一个动点,若三角形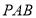 为等腰三角形,则它的底边长为______.
为等腰三角形,则它的底边长为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数图像经过
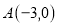 和
和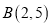 两点
两点(1)求这个函数解析式;
(2)过点B作直线与
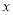 轴交于点
轴交于点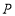 ,若三角形
,若三角形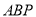 的面积为10,试求点P的坐标.
的面积为10,试求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位招聘员工,采取笔试与面试相结合的方式,两项成绩的原始分均为100分,前6名选手的得分如下:

根据规定,笔试成绩和面试成绩按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)
(1)这6名选手笔试成绩的平均数是_____分,中位数是_____分,众数是______分.
(2)现已知1号选手的综合成绩为88分,求笔试成绩和面试成绩的百分比各为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和妈妈购物后回家,在一楼电梯口看到电梯正显示在顶楼(9楼),他们等了18s后,电梯显示在7楼,这时小明选择走楼梯,高度上升的速度为
 ,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).
,他妈妈则继续等电梯,结果两个人同时到达家所在的楼层。图中所示的细线、粗线分别表示电梯匀速升降、小明走楼梯与一楼地面的距离h(m)与时间t(s)之间的关系。(温馨提示:小明家所在的电梯楼房为3m一层,人们进出电梯所用时间忽略不计,楼层与楼高的关系).
(1)写出A,B两点的坐标;
(2)写出直线AB的解析式,并解释点C的实际意义;
(3)求a,b的值,并求出小明家所处的楼层.
-
科目: 来源: 题型:
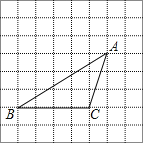
查看答案和解析>>【题目】如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
(1)动手操作:按上面步骤作出经过两次平移后分别得到的三角形;
(2)设AC与DE相交于点M,则图中与∠BAC相等的角有 个;
(3)若∠BAC=43°,∠B=32°,则∠PHG= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
相关试题

