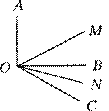
【题目】(1)已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,求∠MON与∠AOB的关系.
(2)如果(1)中,改变∠AOB的大小,其他条件不变,求∠MON与∠AOB的关系.
(3)你从(1),(2)的结果中能发现什么规律?
参考答案:
【答案】(1)∠MON=![]() ∠AOB;(2)∠MON=
∠AOB;(2)∠MON=![]() ∠AOB;(3)∠MON总等于∠AOB的一半
∠AOB;(3)∠MON总等于∠AOB的一半
【解析】
试题(1)根据题意,易得∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC进而结合∠MON=∠MOC-∠NOC的关系,易得答案;
∠BOC进而结合∠MON=∠MOC-∠NOC的关系,易得答案;
(2)由(1)的结论,易得改变∠AOB的大小,其他条件不变,总有∠MON=![]() ∠AOB的关系,即可得答案;
∠AOB的关系,即可得答案;
(3)分析(1)(2)的结论,易得答案.
试题解析:(1)∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,
∠BOC,
∴∠MON=∠MOC-∠NOC=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() ∠AOB=
∠AOB=![]() =45°,
=45°,
∴∠MON=![]() ∠AOB;
∠AOB;
(2)改变∠AOB的大小,其他条件不变,总有∠MON=![]() ∠AOB;理由如下:
∠AOB;理由如下:
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ∠AOC,∠NOC= ∠BOC,
∴∠MON=∠MOC-∠NOC= ∠AOC- ∠BOC= ∠AOB;
(3)由(1)(2)的结果,可得出结论:∠MON的大小总等于∠AOB的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与y轴交于点C,顶点为D.

(1)求顶点D的坐标.
(2)求△OCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(请用“画树状图”或“列表”等方法写出分析过程);
(2)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 ,求n的值.
,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
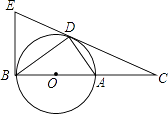
(1)求证:CD是⊙O的切线.
(2)过点B作⊙O的切线交CD的延长线于点E,若OB=5,BC=18,求BE的长. -
科目: 来源: 题型:
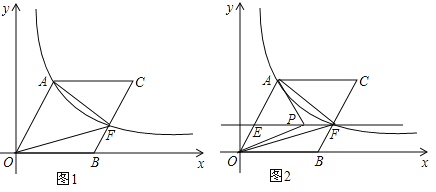
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数
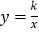 (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;(2)若F为BC的中点,且S△AOF=24
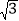 ,求OA长及点C坐标;
,求OA长及点C坐标;(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角
 中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长.
中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长. 
相关试题

