【题目】如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:

(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为![]() ,且点B在格点上;
,且点B在格点上;
(2)以上题中所画线段AB为一边,另外两条边长分别是3,![]() ,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
(3)所画的三角形ABC的AB边上高线长为_________(直接写出答案)
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据勾股定理可知使线段AB为直角边为2和1的直角三角形的斜边即可;
(2)作出另外两条边长分别是3,![]() ,的三角形ABC即可;
,的三角形ABC即可;
(3)根据三角形的面积公式即可得到所画的三角形ABC的AB边上高线长.
(1)如图所示:
(2)如图所示:
(3)三角形ABC的AB边上高线长为:![]() .
.
故答案为:.![]()
-
科目: 来源: 题型:
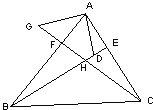
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
-
科目: 来源: 题型:
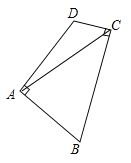
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .
-
科目: 来源: 题型:
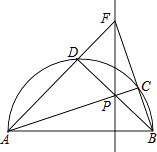
查看答案和解析>>【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( ) ①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.
A.①③
B.①④
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图①,当点D在线段BC上时。
①BC与CF的位置关系为:___;
②BC,CD,CF之间的数量关系为:___;(将结论直接写在横线上)
(2)数学思考
如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图③,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=
 ,CD=
,CD= BC,请求出GE的长。
BC,请求出GE的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2 , 若
 =0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1)
=0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1) 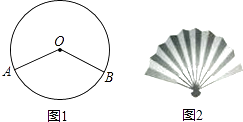
-
科目: 来源: 题型:
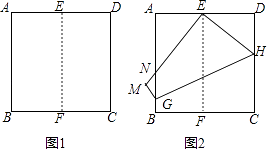
查看答案和解析>>【题目】如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE= .
相关试题

