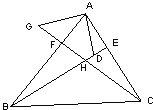
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)AD⊥AG,证明见解析.
【解析】试题分析:(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.
试题解析:(1)∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,
又∵∠BHF=∠CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
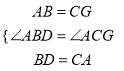 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等);
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若上升15米记作+15米,则-9米表示__________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,3,5,4,4,6的中位数和平均数分别是( )
A.4.5和4 B.4和4 C.4和4.8 D.5和4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制成如下不完整的条形统计图和扇形统计图.
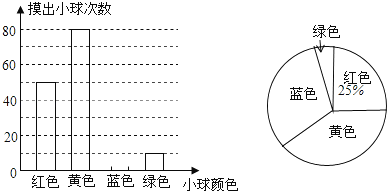
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把三角形的面积分为相等的两部分的是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 2 cm ,3 cm,5 cm B. 3 cm,3 cm,6 cm
C. 5 cm,8 cm,2 cm D. 4 cm,5 cm,6 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为3和6,则它的周长等于_______。
相关试题

