【题目】如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2 , 若 ![]() =0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1)
=0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为°.(精确到0.1) 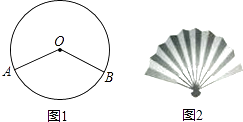
参考答案:
【答案】137.5
【解析】解:设“黄金扇形的”的圆心角是n°,扇形的半径为r, 则 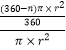 =0.618,
=0.618,
解得:n≈137.5,
所以答案是:137.5.
【考点精析】本题主要考查了扇形面积计算公式和黄金分割的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( ) ①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.
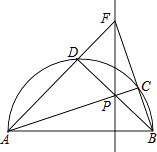
A.①③
B.①④
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:

(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为
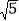 ,且点B在格点上;
,且点B在格点上;(2)以上题中所画线段AB为一边,另外两条边长分别是3,
 ,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);(3)所画的三角形ABC的AB边上高线长为_________(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图①,当点D在线段BC上时。
①BC与CF的位置关系为:___;
②BC,CD,CF之间的数量关系为:___;(将结论直接写在横线上)
(2)数学思考
如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图③,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=
 ,CD=
,CD= BC,请求出GE的长。
BC,请求出GE的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE= .
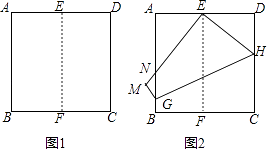
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据以下10个乘积,回答问题:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;(1)试将以上各乘积分别写成一个平方差的形式,并写出其中一个的思考过程
(2)将以上10个乘积按照从小到大排列起来
(3)若用
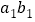 ,
,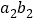 ,
,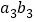 ,....
,.... ,表示n个乘积,其中
,表示n个乘积,其中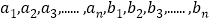 为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明)
为正数,试由(1)(2)猜测一个一般性的结论。(不要求写证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】我市启动了第二届“美丽港城,美在阅读”全民阅读活动,为了解市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
阅读时间
x(min)0≤x<30
30≤x<60
60≤x<90
x≥90
合计
频数
450
400
50
频率
0.4
0.1
1
(1)补全表格;
(2)将每天阅读时间不低于60min的市民称为“阅读爱好者”,若我市约有500万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
相关试题

