【题目】如图,在△ABC中,AB=30 cm,BC=35 cm,∠B=60°,有一动点M自A向B以1 cm/s的速度运动,动点N自B向C以2 cm/s的速度运动,若M,N同时分别从A,B出发.
(1)经过多少秒,△BMN为等边三角形;
(2)经过多少秒,△BMN为直角三角形.

参考答案:
【答案】(1) 出发10s后,△BMN为等边三角形;(2)出发6s或15s后,△BMN为直角三角形.
【解析】
(1)设时间为x,表示出AM=x、BN=2x、BM=30-x,根据等边三角形的判定列出方程,解之可得;
(2)分两种情况:①∠BNM=90°时,即可知∠BMN=30°,依据BN=![]() BM列方程求解可得;②∠BMN=90°时,知∠BNM=30°,依据BM=
BM列方程求解可得;②∠BMN=90°时,知∠BNM=30°,依据BM=![]() BN列方程求解可得.
BN列方程求解可得.
解 (1)设经过x秒,△BMN为等边三角形,
则AM=x,BN=2x,
∴BM=AB-AM=30-x,
根据题意得30-x=2x,
解得x=10,
答:经过10秒,△BMN为等边三角形;
(2)经过x秒,△BMN是直角三角形,
①当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=30°,
∴BN=![]() BM,即2x=
BM,即2x=![]() (30-x),
(30-x),
解得x=6;
②当∠BMN=90°时,
∵∠B=60°,
∴∠BNM=30°,
∴BM=![]() BN,即30-x=
BN,即30-x=![]() ×2x,
×2x,
解得x=15,
答:经过6秒或15秒,△BMN是直角三角形.
故答案为:(1)10.(2)6或15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-5.5)+(-3.2)-(-2.5)-4.8
(2)-40-28-(-19)+(-24)
(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

-
科目: 来源: 题型:
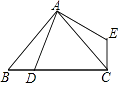
查看答案和解析>>【题目】如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=
 .其中正确的是________(填序号).
.其中正确的是________(填序号).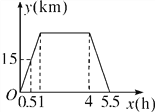
相关试题

