【题目】如图,直线y=kx﹣1与x轴、y轴分别交于B、C两点,且3BO﹣![]() CO=1
CO=1
(1)求点B的坐标及k的值;
(2)若点A(x,y)是第一象限内的直线y=kx﹣1上的一个动点,在点A的运动过程中,试写出△AOB的面积S与x之间的函数解析式;
(3)探索:当点A运动到什么位置时,△AOB的面积是![]() ?
?

参考答案:
【答案】(1)k=2,B(![]() ,0);
,0);
(2)S=![]() x﹣
x﹣![]() (x>
(x>![]() );
);
(3)A点运动到(4,1)或(0,1)位置时,△AOB的面积是![]() .
.
【解析】试题分析:(1)利用坐标轴上点的坐标特征和一次函数图象上点的坐标特征先得到C(0,-1),B(![]() ,0),则利用3BO-
,0),则利用3BO-![]() CO=1得到
CO=1得到![]() -
-![]() =1,解方程得到k的值,从而得到B点坐标;(2)A点坐标表示为(x,
=1,解方程得到k的值,从而得到B点坐标;(2)A点坐标表示为(x, ![]() x-1),然后利用三角形面积公式求解;(3)设A(x,
x-1),然后利用三角形面积公式求解;(3)设A(x, ![]() x-1),利用三角形面积公式得到
x-1),利用三角形面积公式得到![]() |
|![]() x-1|=
x-1|=![]() ,然后解绝对值方程得到x的值,从而得到A点坐标.
,然后解绝对值方程得到x的值,从而得到A点坐标.
试题解析:当x=0时,y=kx﹣1=﹣1,则C(0,﹣1),
当y=0时,kx﹣1=0,解得x=![]() ,则B(
,则B(![]() ,0),
,0),
∵3BO﹣![]() CO=1
CO=1
∴![]() ﹣
﹣![]() =1,
=1,
∴k=2,
∴B(![]() ,0);
,0);
(2)y=![]() x﹣1,
x﹣1,
S=![]()
![]() (
(![]() x﹣1)
x﹣1)
=![]() x﹣
x﹣![]() (x>
(x>![]() );
);
(3)设A(x, ![]() x﹣1),
x﹣1),
∵S=![]()
![]() |
|![]() x﹣1|,
x﹣1|,
∴![]() |
|![]() x﹣1|=
x﹣1|=![]() ,解得x=4或x=0,
,解得x=4或x=0,
∴A点坐标为(4,1)或(0,1),
即A点运动到(4,1)或(0,1)位置时,△AOB的面积是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:
 表示 5与2两个数在数轴上所对应的两个点之间的距离,探索:
表示 5与2两个数在数轴上所对应的两个点之间的距离,探索:(1)
 =_________;
=_________;(2)如果
 请写出x的值;
请写出x的值;(3)求适合条件
 的所有整数x的值;
的所有整数x的值;(4)利用数轴, 求满足
 的整数x的值.
的整数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,若∠A+∠C=160°,则∠B=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(x﹣2)2=3(x﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴交于点P,直线y=
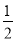 x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式.
x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
相关试题

