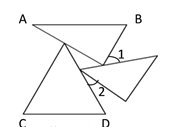
【题目】一个正三角形和一副三角板(分别含30°和45°)摆放成如图所示的位置,且AB∥CD.则∠1+∠2=__________.
参考答案:
【答案】75°
【解析】
连接AC,根据平行线的性质求出∠BAC+∠ACD=180°,再由∠BAG=30°,∠ECD=60°可得出∠EAC+∠ACE的度数,根据三角形内角和定理得出∠AEC的度数,由补角的定义得出∠GEF的度数,同理可用∠1表示出∠EGF,用∠2表示出∠GFE,再由三角形内角和定理即可得出结论.
解:连接AC,
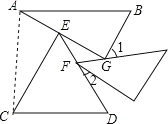
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠BAG=30°,∠ECD=60°,
∴∠EAC+∠ACE=180°-30°-60°=90°,
∵∠CED=60°,
∴∠GEF=180°-90°-60°=30°,
同理∠EGF=180°-∠1-90°=90°-∠1,∠GFE=180°-45°-∠2=135°-∠2,
∵∠GEF+∠EGF+∠GFE=180°,即30°+90°-∠1+135°-∠2=180°,解得∠1+∠2=75°.
故答案为:75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某加工厂加工一批绿色蔬菜,若12个大加工车间和15个小加工车间一天同时加工,则可加工绿色蔬菜1575吨;若3个大加工车间和5个小加工车间一天同时加工,则可加工绿色蔬菜450吨.
(1)每个大车间和每个小车间每天各加工多少吨绿色蔬菜?
(2)若该工厂有25个大加工车间,20个小加工车间;每个大车间每天耗费3000元,每个小车间每天耗费2500元,现有2250吨绿色蔬菜,要求一天之内加工完,如何分配车间才能更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点P是AB的中点,
 的延长线于点E,连接AE,过点A作
的延长线于点E,连接AE,过点A作 交DP于点F,连接BF、
交DP于点F,连接BF、 下列结论中:
下列结论中: ≌
≌ ;
; ;
; 是等边三角形;
是等边三角形; ;
; 其中正确的是
其中正确的是


A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:解不等式和方程组
(1)解不等式:5+x≥3(x﹣1);
(2)解方程组: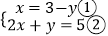 .
. -
科目: 来源: 题型:
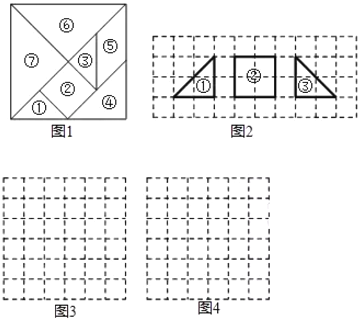
查看答案和解析>>【题目】七巧板又称智慧板,是中国民间流传的智力玩具,它是由七块板组成(如图1),用这七块板可拼出许多图形(1600种以上),例如:三角形、平行四边形、以及不规则的多边形,它还可以拼出各种人物、动物、建筑等.请你用七巧板中标号为①②③的三块板(如图2经过平移、旋转拼出下列图形(相邻两块板之间无空隙,无重叠;示意图的顶点画在小方块顶点上):
(1)拼成长方形,在图3中画出示意图;
(2)拼成等腰直角三角形,在图4中面出示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
30秒跳绳次数的频数、频率分布表成绩段
频数
频率
0≤x<20
5
0.1
20≤x<40
10
a
40≤x<60
b
0.14
60≤x<80
m
c
80≤x<100
12
n
根据以上图表信息,解答下列问题:
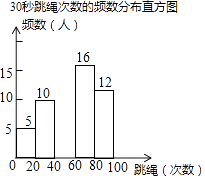
(1)表中的a= , m=;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
相关试题

