搜索
【题目】如图，在平面直角坐标系xOy中，过坐标原点O的直线l与双曲线y= 
相交于点A（m，3）．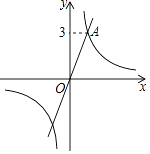 
（1）求直线l的表达式；
（2）过动点P（n，0）且垂于x轴的直线与l及双曲线的交点分别为B，C，当点B位于点C上方时，写出n的取值范围 ．
参考答案：
【答案】
（1）解：∵双曲线y= 
过点A（m，3），
∴3=3m，解得：m=1，
∴点A的坐标为（1，3）．
设直线l的表达式为y=kx，
将（1，3）代入y=kx中，3=k，
∴直线l的表达式为y=3x
（2）解：﹣1＜n＜0或n＞1
【解析】解： （2）由正、反比例函数的对称性可知：直线l与双曲线y= 的两交点坐标为（﹣1，﹣3）和（1，3）． 观察函数图象可知：当﹣1＜x＜0或x＞1时，一次函数图象在双曲线的上方，
∴n的取值范围为﹣1＜n＜0或n＞1．
所以答案是：﹣1＜n＜0或n＞1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．
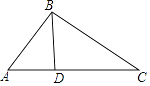
（1）求证：△CBD∽△CAB；
（2）若D是AC中点，CD=3，求BC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数y=
的图象经过点P（﹣1，﹣1）．
（1）求此函数的表达式；
（2）画出此函数在第一象限内的图象．
（3）根据函数图象写出此函数的一条性质． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD∽四边形EFGH，连接相应的对角线AC，EG．
（1）求证△ABC∽△EFG；
（2）若
= 
，直接写出四边形ABCD与四边形EFGH的面积比为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】若平面直角坐标系中的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．
（1）若动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为 ， 点G的坐标为 ．
（2）若动点P从坐标原点出发，先按照“平移量”m平移到B，再按照“平移量”n平移到C；最后按照“平移量”q平移回到点O．当△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，请你直接写出“平移量”m ， n ， q ．
（3）在（1）、（2）的前提下，请你在平面直角坐标系中画出△OBC与△MNG． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=mx2+（3m+1）x+3．
（1）当m取何值时，此二次函数的图象与x轴有两个交点；
（2）当抛物线y=mx2+（3m+1）x+3与x轴两个交点的横坐标均为整数，且m为正整数时，求此抛物线的表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．
（1）如图1，当点D是BC边上的中点时，S△ABD：S△ACD=；
（2）如图2，当AD是∠BAC的平分线时，若AB=m，AC=n，求S△ABD：S△ACD的值（用含m，n的代数式表示）
（3）如图3，AD平分∠BAC，延长AD到E，使得AD=DE，连接BE，如果AC=2，AB=4，S△BDE=6，那么S△ABC= ．
相关试题
