搜索
【题目】已知反比例函数y= 
的图象经过点P（﹣1，﹣1）．
（1）求此函数的表达式；
（2）画出此函数在第一象限内的图象．
（3）根据函数图象写出此函数的一条性质．
参考答案：
【答案】
（1）解：∵反比例函数y= 
的图象经过点P（﹣1，﹣1）．
∴﹣1= 
，解得k=1．
∴此函数的表达式为y= 
（2）解：函数在第一象限内的图象如图：
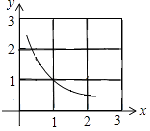
（3）解：函数在第一象限，y随x的增大而减小
【解析】（1）直接把点P（﹣1，﹣1）代入反比例函数y= ，利用待定系数法求得即可；（2）根据反比例函数的解析式，然后作出其图象即可；（3）根据图象结合反比例函数的性质即可求解．
【考点精析】关于本题考查的反比例函数的图象，需要了解反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AC和直线l分别垂直线段AB于点A，B．点P是线段AB上的一个动点，由A移动到B，连接CP，过点P作PD⊥CP交l于点D，设线段AP的长为x，BD的长为y，在下列图象中，能大致表示y与x之间函数关系的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在反比例函数y=
（x＞0）的图象上，有点P1 ， P2 ， P3 ， P4…Pn（n为正整数，且n≥1）．它们的横坐标依次为1，2，3，4…n（n为正整数，且n≥1），分别过这些点作x轴与y轴的垂线，连接相邻两点，图中所构成的阴影部分的面积从左到右依次为S1 ， S2 ， S3…Sn﹣1（n为正整数，且n≥2），那么S2+S3+S4+…S7= ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．
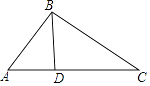
（1）求证：△CBD∽△CAB；
（2）若D是AC中点，CD=3，求BC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD∽四边形EFGH，连接相应的对角线AC，EG．
（1）求证△ABC∽△EFG；
（2）若
= 
，直接写出四边形ABCD与四边形EFGH的面积比为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，过坐标原点O的直线l与双曲线y=
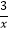相交于点A（m，3）．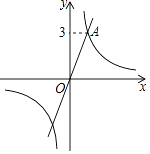 
（1）求直线l的表达式；
（2）过动点P（n，0）且垂于x轴的直线与l及双曲线的交点分别为B，C，当点B位于点C上方时，写出n的取值范围 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】若平面直角坐标系中的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．
（1）若动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为 ， 点G的坐标为 ．
（2）若动点P从坐标原点出发，先按照“平移量”m平移到B，再按照“平移量”n平移到C；最后按照“平移量”q平移回到点O．当△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，请你直接写出“平移量”m ， n ， q ．
（3）在（1）、（2）的前提下，请你在平面直角坐标系中画出△OBC与△MNG．
相关试题
