【题目】如图,直线AB:y=一 ![]() x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ![]() ),与直线AB交于点E.
),与直线AB交于点E.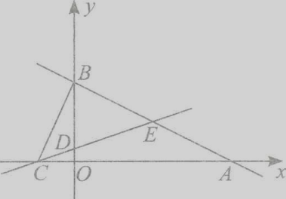
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
参考答案:
【答案】
(1)解:设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: 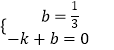
∴ ![]()
∴直线 ![]() 表达式为:
表达式为: ![]()
(2)解:∵ 
∴ ![]() , ∴E(2,1),
, ∴E(2,1),
∵C(-1,0),A(4,0),
∴A C=5, OB=2, ![]()
∴ ![]()
![]()
![]()
![]()
(3)解:点 ![]() 关于直线
关于直线 ![]() 的对称点为
的对称点为 ![]() ,连接
,连接 ![]() 交直线
交直线 ![]() 于点
于点 ![]() ,则点
,则点 ![]() 即为所求的点
即为所求的点

设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: ![]()
∴ ![]()
∴ ![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]() ∴
∴ ![]()
∴m= ![]()
【解析】(1)设直线 C D 表达式为: y = k x + b,用待定系数法即可求出直线CD的解析式 ;
(2)首先解直线AB与直线CD的解析式联立的方程组求出E点的坐标,根据A,B,C,E四点的坐标得出AC,OB的长,及E点到y轴的距离,根据 S Δ B C E = S Δ A B C S Δ A C E带值计算即可;
(3) E 关于直线 y = 2 的对称点为 E’ ( 2 , 3 ) ,连接 A E’交直线 y = 2 于点 Q ,则点 Q 即为所求的点,用待定系数法求出直线 A E’的解析式,然后把y=2代入直线 A E’的解析式求出对应的x的值,从而得出Q点的坐标,得到m的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G.
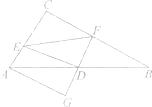
(1)求证:AG=BF;
(2)若AE=4,BF=8,求线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】81的算术平方根是( )
A. 9B. -9C. ±9D. 不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
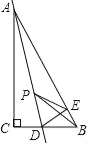
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
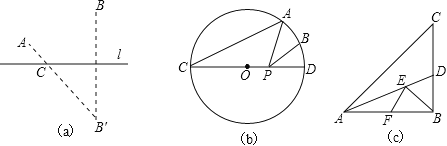
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“同角的余角相等”改成“如果...,那么....”的形式.如果____________,那么______________。
相关试题

