【题目】如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G.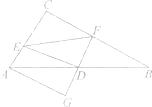
(1)求证:AG=BF;
(2)若AE=4,BF=8,求线段EF的长.
参考答案:
【答案】
(1)证明:∵D是AB的中点,
∴AD=BD.
∵AG∥BC,
∴∠GAD=∠FBD.
∵∠ADG=∠BDF,
∴△ADG≌△BDF.
∴AG=BF.
(2)解:连接EG,
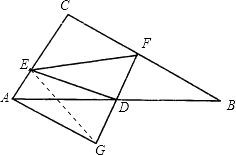
∵△ADG≌△BDF,
∴GD=FD.
∵DE⊥DF,
∴EG=EF.
∵AG∥BC,∠ACB=90°,
∴∠EAG=90°.
在Rt△EAG中,
∵EG2=AE2+AG2=AE2+BF2
∴EF2=AE2+BF2且AE=4,BF=8.
∴EF=4 ![]() .
.
【解析】(1)根据中点的定义得出AD=BD ,根据平行线的性质得出∠GAD=∠FBD,根据对顶角相等得出∠ADG=∠BDF ,从而用ASA判断出△ADG≌△BDF,根据全等三角形对应边相等得出AG=BF ;
(2)连接EG,由三角形全等得出GD=FD ,根据中垂线的性质得出EG=EF ,根据二直线平行同旁内角互补得出∠EAG=90°.在Rt△EAG中,根据勾股定理及等量代换得出EF2=AE2+BF2 ,从而代指计算得出EF的长。
【考点精析】解答此题的关键在于理解线段的中点的相关知识,掌握线段的中点到两端点的距离相等,以及对平行线的性质的理解,了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(4,﹣1)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植树4~7棵,活动结束后随机抽查了20名学生每人的植树数量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的.而条形图尚有一处错误.
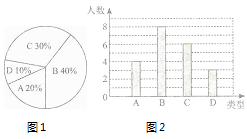
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】81的算术平方根是( )
A. 9B. -9C. ±9D. 不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=一
 x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,  ),与直线AB交于点E.
),与直线AB交于点E.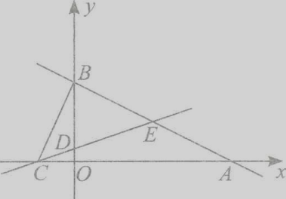
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
相关试题

