【题目】某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)若某月用水12吨,应交水费多少元?
参考答案:
【答案】
(1)解:设每吨水的基础价为a元,调节价为b元,
根据题意得: ![]() ,
,
解得: ![]() ,
,
则每吨水的基础价和调节价分别为1元和1.3元
(2)解:![]()
(3)解:根据题意得:1.3×12﹣3=12.6(元),
则应交水费为12.6元
【解析】(1)设每吨水的基础价为a元,调节价为b元,根据第一个月用水16吨,需交水费17.8元及第二个月用水20吨,需交水费23元 ,列出方程组求解即可 ;
(2)分段讨论:①当0<x≤10时,y=x ; ②当x>10时,y=10+1.3×(x-10) ;
(3)把x=12代入y=10+1.3×(x-10)计算即可得出答案。
-
科目: 来源: 题型:
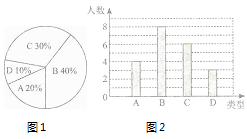
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植树4~7棵,活动结束后随机抽查了20名学生每人的植树数量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的.而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G.
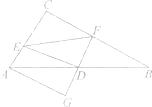
(1)求证:AG=BF;
(2)若AE=4,BF=8,求线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】81的算术平方根是( )
A. 9B. -9C. ±9D. 不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=一
 x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,  ),与直线AB交于点E.
),与直线AB交于点E.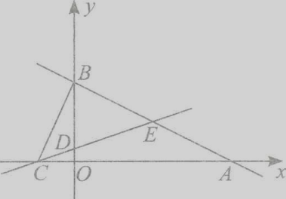
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
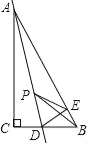
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
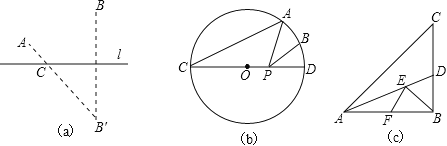
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为 .
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
相关试题

