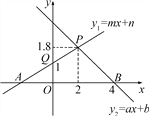
【题目】如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是________;
(2)关于x的不等式mx+n<1的解集是________;
(3)当x为何值时,y1≤y2?
(4)当x<0时,比较y2与y1的大小关系.
参考答案:
【答案】(1)x<4;(2)x<0;(3) x≤2;(4)y2>y1.
【解析】试题分析:(1)利用直线y2=ax+b与x轴的交点为(4,0),然后利用函数图象可得到不等式ax+b>0的解集.
(2)利用直线y=mx+n与x轴的交点为(0,1),然后利用函数图象可得到不等式mx+n<1的解集.
(3)结合两条直线的交点坐标为(2,1.8)来求得y1≤y2解集.
(4)结合函数图象直接写出答案.
试题解析:(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4;
故答案是:x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0;.
故答案是:x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,
所以当x≤2时,y1≤y2;
(4)如图所示,当x<0时,y2>y1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

-
科目: 来源: 题型:
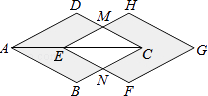
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC=4cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为 .
-
科目: 来源: 题型:
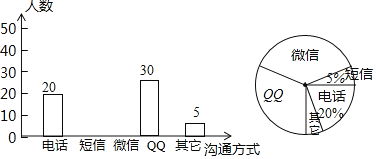
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样.便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了_______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为__________;
(2)某天甲同学想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与乙同学联系,恰好选用“微信”联系的概率为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.

(1)点B到OM的距离等于;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
与y=m﹣x的图象的一个交点是A(2,3),其中k、m为常数.
(1)求k、m的值,画出函数的草图.
(2)根据图象,确定自变量x的取值范围,使一次函数的函数值大于反比例函数的函数值.
相关试题

