Question

【题目】如图，已知△ABC中，∠B=∠C，AB=AC=10cm，BC=8cm，点D为AB的中点．

（1）如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．

①若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC边上相遇？

Answer 1

【答案】（1）全等，理由见解析；（2），（3）.

【解析】试题分析：（1）①根据时间和速度分别求得两个三角形中的边的长，根据SAS判定两个三角形全等．

②根据全等三角形应满足的条件探求边之间的关系，再根据路程=速度×时间公式，先求得点P运动的时间，再求得点Q的运动速度；

（2）根据题意结合图形分析发现：由于点Q的速度快，且在点P的前边，所以要想第一次相遇，则应该比点P多走等腰三角形的两个腰长．

试题解析：（1）①∵t=1s，

∴BP=CQ=3×1=3cm，

∵AB=10cm，点D为AB的中点，

∴BD=5cm．

又∵PC=BC﹣BP，BC=8cm，

∴PC=8﹣3=5cm，

∴PC=BD．

又∵AB=AC，

∴∠B=∠C，

在△BPD和△CQP中， ，

∴△BPD≌△CQP（SAS）．

②∵vP≠vQ，

∴BP≠CQ，

若△BPD≌△CPQ，∠B=∠C，

则BP=PC=4cm，CQ=BD=5cm，

∴点P，点Q运动的时间，

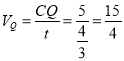∴cm/s；

（2）设经过x秒后点P与点Q第一次相遇，

由题意，得x=3x+2×10，

解得．

∴点P共运动了×3=80cm．

△ABC周长为：10+10+8=28cm，

若是运动了三圈即为：28×3=84cm，

∵84﹣80=4cm＜AB的长度，

∴点P、点Q在AB边上相遇，

∴经过s点P与点Q第一次在边AB上相遇．