【题目】如图,菱形ABCD的对角线AC=4cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为 . 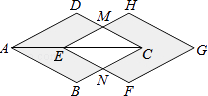
参考答案:
【答案】![]()
【解析】解:∵ME∥AD, ∴△MEC∽△DAC,
∴ ![]() ,
,
∵菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,
∴AE=1cm,EC=3cm,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴图中阴影部分图形的面积与四边形EMCN的面积之比为: ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用菱形的性质和平移的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司要将一批货物运往某地,打算租用某汽车运输公司的甲.乙两种货车,以前租用这两种货车的信息如下表所示;
第一次
第二次
甲种货车辆数/辆
2
5
乙种货车辆数/辆
3
6
累计运货量/吨
15.5
35
现打算租用该公司4辆甲种货车和6辆乙种货车,可一次刚好运完这批货物.如果每吨运费为50元,该公司应付运费________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

-
科目: 来源: 题型:
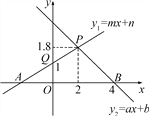
查看答案和解析>>【题目】如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是________;
(2)关于x的不等式mx+n<1的解集是________;
(3)当x为何值时,y1≤y2?
(4)当x<0时,比较y2与y1的大小关系.
-
科目: 来源: 题型:
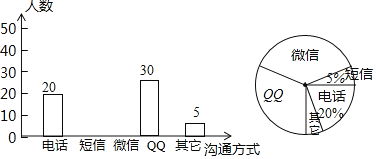
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样.便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次统计共抽查了_______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为__________;
(2)某天甲同学想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与乙同学联系,恰好选用“微信”联系的概率为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.

(1)点B到OM的距离等于;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的.
相关试题

