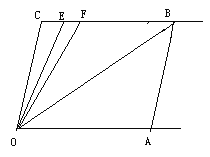
【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
参考答案:
【答案】(1)30°;(2)1:2;(3)45°.
【解析】
(1)根据两直线平行,同旁内角互补求出∠AOC,再根据角平分线的定义求出∠EOB=![]() ∠AOC,代入数据即可得解;
∠AOC,代入数据即可得解;
(2)根据两直线平行,内错角相等可得∠OBC=∠BOA,从而得到∠OBC=∠FOB,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OFC=2∠OBC,从而得解;
(3)设∠AOB=x,根据两直线平行,内错角相等表示出∠CBO=∠AOB=x,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC,然后利用三角形的内角和等于180°列式表示出∠OBA,然后列出方程求解即可.
(1)∵CB∥OA,∴∠AOC=180°-∠C=180°-120°=60°.
∵∠FOB=∠AOB,OE平分∠COF,∴∠EOB=![]() ∠AOC=
∠AOC=![]() ×60°=30°;
×60°=30°;
(2)∠OBC:∠OFC的值不会发生变化,为1:2.
∵CB∥OA,∴∠OBC=∠BOA.
∵∠FOB=∠AOB,∴∠OBC=∠FOB,∴∠OFC=∠OBC+∠FOB=2∠OBC,∴∠OBC:∠OFC=1:2;
(3)当平行移动AB至∠OBA=45°时,∠OEC=∠OBA.
设∠AOB=x.
∵CB∥AO,∴∠CBO=∠AOB=x.
∵∠OEC=∠CBO+∠EOB=x+30°,∠OBA=180°-∠A-∠AOB=180°-120°-x=60°-x,∴x+30°=60°-x,∴x=15°,∴∠OEC=∠OBA=60°-15°=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了名同学;
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将三角形ABC向左平移至点B与原点重合,得三角形A′OC′.
(1)直接写出三角形ABC的三个顶点的坐标A ,B ,C ;
(2)画出三角形A′OC′;
(3)求三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b和反比例函数y
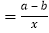 在同一直角坐标系中的大致图象是( )
在同一直角坐标系中的大致图象是( )A.
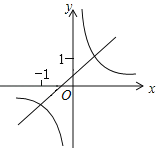 B.
B. 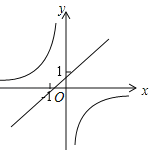
C.
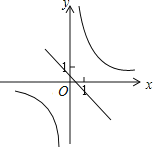 D.
D. 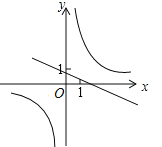
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,点
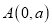 、
、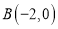 、
、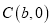 且
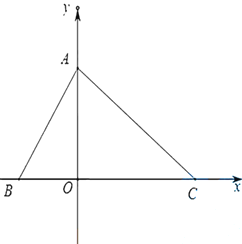
且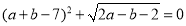 ,
,
(1)求点
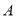 、
、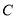 的坐标;
的坐标;(2)求
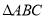 的面积
的面积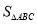 ;
;(3)当点
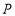 的坐标是
的坐标是 且
且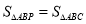 时,求
时,求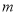 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题“已知
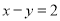 且
且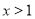 ,
,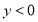 ,试确定
,试确定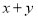 的取值范围”有如下解法:
的取值范围”有如下解法:解:
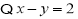
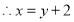
又
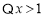
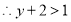
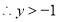 又
又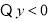
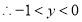 ①
①同理得:
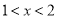 ②
②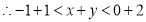 即
即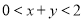 ,
,请按照上述方法,完成下列问题:
(1)已知关于
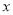 、
、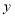 的方程组
的方程组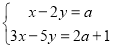 的解均为负数,若
的解均为负数,若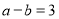 且
且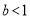 ,求
,求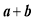 的取值范围.
的取值范围.(2)已知
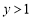 ,
,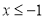 ,若
,若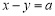 成立,求
成立,求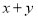 的取值范围(结果用含
的取值范围(结果用含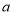 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
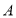 的坐标为
的坐标为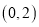 ,将点
,将点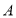 向右平移
向右平移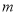 个单位得到点
个单位得到点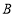 ,其中关于
,其中关于 的一元一次不等式
的一元一次不等式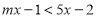 的解集为
的解集为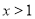 ,过点
,过点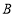 作
作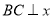 轴于
轴于 得到长方形
得到长方形 ,
,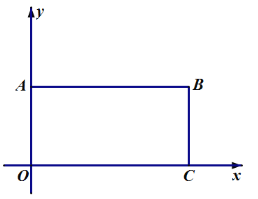
(1)求
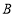 点坐标______及四边形
点坐标______及四边形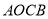 的面积_______;
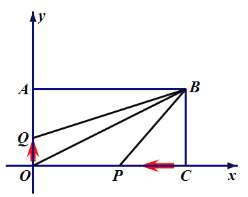
的面积_______;(2)如图2,点
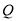 从
从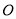 点以每秒
点以每秒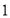 个单位长度的速度在
个单位长度的速度在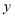 轴上向上运动,同时点
轴上向上运动,同时点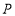 从
从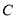 点以每秒
点以每秒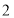 个单位长度的速度匀速在
个单位长度的速度匀速在 轴上向左运动,设运动的时间为
轴上向左运动,设运动的时间为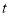 秒
秒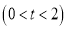 ,问是否存在一段时间,使得
,问是否存在一段时间,使得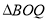 的面积不大于
的面积不大于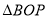 的面积,若存在,求出
的面积,若存在,求出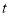 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;(3)在(2)的条件下,四边形
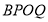 的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
相关试题

