【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() 得到长方形
得到长方形![]() ,
,
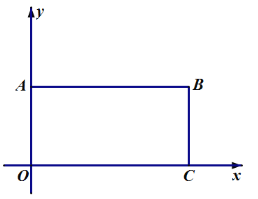
(1)求![]() 点坐标______及四边形
点坐标______及四边形![]() 的面积_______;
的面积_______;
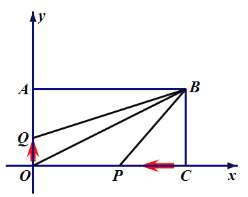
(2)如图2,点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度在
个单位长度的速度在![]() 轴上向上运动,同时点
轴上向上运动,同时点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度匀速在
个单位长度的速度匀速在![]() 轴上向左运动,设运动的时间为
轴上向左运动,设运动的时间为![]() 秒
秒![]() ,问是否存在一段时间,使得
,问是否存在一段时间,使得![]() 的面积不大于
的面积不大于![]() 的面积,若存在,求出
的面积,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,四边形![]() 的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)存在,
;(2)存在,![]() ;(3)不变;值为
;(3)不变;值为![]() .
.
【解析】
(1)利用不等式求出m的值,结合平移的性质得出B、C点坐标,再利用矩形面积求法得出答案;
(2)利用Q,P点移动速度分别表示出△BOQ和△BOP的面积,进而得出t的取值范围,即可得出答案;
(3)利用![]()
(1)由![]() 得,
得,![]()
∵不等式![]() 的解集为
的解集为![]()
∴![]()
解得m= 4
∵点A的坐标为(0, 2), 且向右平移b个单位得到点B
∴B(4, 2)
∵BC⊥x轴于C
∴C(4,0)
∵AB//OC,∠AOC=∠BCO = 90°
∴∠B+∠OCB = 180°
∴∠B=90°
∴四边形AOCB是矩形
∴![]()
故答案为:![]() ;
;![]() ;
;
(2)存在,理由如下:
由题意知: OQ= t,CP= 2t
∵四边形AOCB是矩形,OC= 4
∴∠BAO=∠BCO= 90°,OP=4- 2t
∴AB⊥OA,BC⊥OC
∵ ![]()
若![]() 的面积不大于
的面积不大于![]() 的面积.则
的面积.则![]()
解得:![]()
∵t>0
∴![]()
(3)不变,理由如下:
∵![]()
∴![]()
= 2t+4- 2t
=4
-
科目: 来源: 题型:
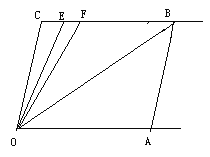
查看答案和解析>>【题目】如图,直线CB∥OA,∠C=∠A=120°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,点
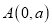 、
、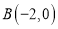 、
、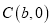 且
且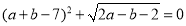 ,
,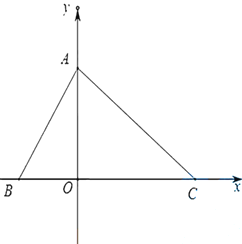
(1)求点
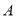 、
、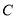 的坐标;
的坐标;(2)求
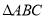 的面积
的面积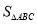 ;
;(3)当点
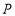 的坐标是
的坐标是 且
且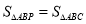 时,求
时,求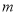 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题“已知
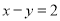 且
且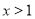 ,
,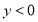 ,试确定
,试确定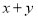 的取值范围”有如下解法:
的取值范围”有如下解法:解:
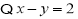
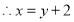
又
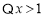
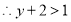
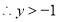 又
又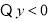
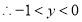 ①
①同理得:
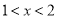 ②
②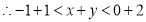 即
即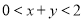 ,
,请按照上述方法,完成下列问题:
(1)已知关于
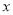 、
、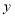 的方程组
的方程组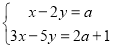 的解均为负数,若
的解均为负数,若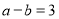 且
且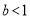 ,求
,求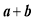 的取值范围.
的取值范围.(2)已知
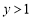 ,
,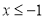 ,若
,若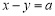 成立,求
成立,求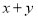 的取值范围(结果用含
的取值范围(结果用含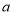 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
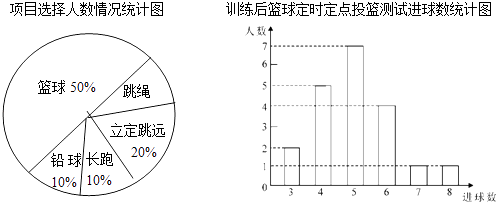
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树状图的方法求恰好选中两名男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次试验中,小明把一根弹簧的上端固定,在其下端悬挂物体,测得弹簧的长度
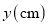 与所挂物体的质量
与所挂物体的质量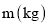 之间的关系如下表:
之间的关系如下表:所挂物体质量
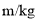
0
1
2
3
4
5
弹簧的长度
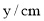
8
10
12
14
16
18
下列说法错误的是( )
A.弹簧的长度随所挂物体质量的变化而变化,所挂物体质量是自变量,弹簧长度是因变量
B.不挂物体时,弹簧的长度为
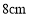
C.弹簧的长度
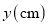 与所挂物体的质量
与所挂物体的质量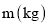 之间的关系式是
之间的关系式是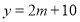
D.在弹性限度内,当所挂物体的质量为
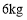 时,弹簧的长度为
时,弹簧的长度为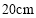
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数 y kx 与 y
 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )
A. 2 B. 4 C. 6 D. 8
相关试题

