【题目】某巡逻车在一条南北大道上巡逻,某天巡逻车从岗亭A处出发,规定向北方向为正,向南方向为负,当天行驶记录如下(单位:千米) ![]() .
.
(1)最终巡逻车是否回到岗亭![]() 处?若没有,请描述巡逻车的位置:
处?若没有,请描述巡逻车的位置:
(2)若巡逻车行驶1千米耗油0.1升,出发时油箱有油5升,请问途中需要加油吗?若需要,途中至少还需补充多少升油?
参考答案:
【答案】(1) 所以最终巡逻车在岗亭![]() 处南方4千米处;(2)油不够,需要补充0.8升
处南方4千米处;(2)油不够,需要补充0.8升
【解析】
(1)计算出八次行车里程的和,看其结果正负情况即可判断位置;
(2)求出所记录的八次行车里程的绝对值的和,再计算油耗,经过比较即可得出答案.
解(1) ![]() (千米)
(千米)
所以最终巡逻车在岗亭![]() 处南方4千米处.
处南方4千米处.
(2)行驶路程:![]() (千米)
(千米)
∴需要油量:![]() (升),
(升),
∵![]() ,
,
故油不够,需要补充0.8升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】依次剪6张正方形纸片拼成如图示意的图形,图形中正方形①的面积为1,正方形②的面积为
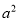 .
.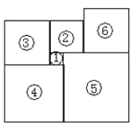
(1)请用含
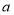 的式子直接写出正方形⑤的面积;
的式子直接写出正方形⑤的面积;(2)若正方形⑥与正方形③的面积相等,求正方形④和正方形⑤的面积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三位数百位上数字是
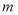 ,十位上数字是
,十位上数字是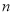 .个位上数字是
.个位上数字是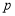 ,则这个三位数可记作
,则这个三位数可记作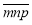
(1)若一个两位数
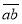 .满足关系式
.满足关系式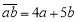 .
.①试求出
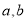 的数量关系:
的数量关系:②请直接写出满足关系式
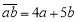 的所有两位数.
的所有两位数.(2)将一个三位数
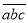 ,其中
,其中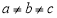 .现将三位数
.现将三位数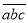 中间数字
中间数字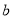 去掉,成为一个两位数
去掉,成为一个两位数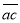 且满足
且满足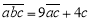 .请直接写出所有符合条件的三位数.
.请直接写出所有符合条件的三位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A. AC,BD互相平分
B. BA=BC
C. AC=BD
D. AB∥CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )

A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=
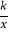 (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣
 t2+5t﹣
t2+5t﹣ )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣ t2+3t﹣
t2+3t﹣ )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣ x2+bx+c的顶点.
x2+bx+c的顶点.①当点P在双曲线y=
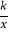 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=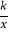 没有公共点;
没有公共点;②当抛物线y=﹣
 x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒
 cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.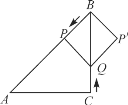
相关试题

