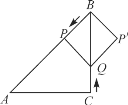
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒![]() cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
参考答案:
【答案】![]()
【解析】
此题先判断出△ABC是等腰直角三角形,再根据等腰直角三角形的性质可得∠ABC=45°,再表示出BP、BQ,然后根据翻折的性质和菱形对角线互相垂直平分列出方程求解即可.
解:如图,
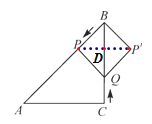
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵点P的速度是每秒![]() cm,点Q的速度是每秒1cm,
cm,点Q的速度是每秒1cm,
∴BP=![]() tcm,BQ=(10﹣t)cm,
tcm,BQ=(10﹣t)cm,
∵四边形QPBP′为菱形,
∴∠BDP=90°,
∴△BDP是等腰直角三角形,
∵BD2+PD2=BP2,
∴BD=![]() BP=
BP=![]() ×
×![]() t=t,
t=t,
∵BD=QD,
∴t=![]() ,
,
解得t=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡逻车在一条南北大道上巡逻,某天巡逻车从岗亭A处出发,规定向北方向为正,向南方向为负,当天行驶记录如下(单位:千米)
 .
.(1)最终巡逻车是否回到岗亭
 处?若没有,请描述巡逻车的位置:
处?若没有,请描述巡逻车的位置:(2)若巡逻车行驶1千米耗油0.1升,出发时油箱有油5升,请问途中需要加油吗?若需要,途中至少还需补充多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )

A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=
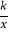 (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣
 t2+5t﹣
t2+5t﹣ )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣ t2+3t﹣
t2+3t﹣ )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣ x2+bx+c的顶点.
x2+bx+c的顶点.①当点P在双曲线y=
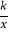 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=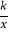 没有公共点;
没有公共点;②当抛物线y=﹣
 x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

-
科目: 来源: 题型:
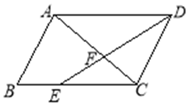
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,若S△EFC=8,则S△CFD=________.
-
科目: 来源: 题型:
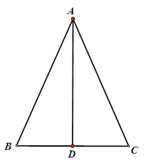
查看答案和解析>>【题目】求证:角平分线和中线重合的三角形是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
相关试题

