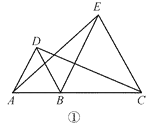
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
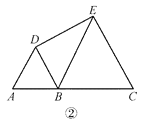
(2)如图②,若 AB=1,BC=2,求 DE 的长;
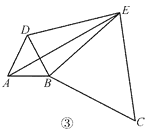
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
参考答案:
【答案】见解析
【解析】试题分析:(1)由△ABD和△ECB都是等边三角形可得AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,所以∠ABE=∠DBC,所以△ABE≌△DBC,即可证明AE=DC;(2)
如图②中,取BE中点F,连接DF,由题意不难得出BF=EF=1=BD,再结合∠DBF=60°可得△DBF是等边三角形,进而推出∠EDB=90°,再由勾股定理可求出DE的长;(3)如图③中,连接DC,由已知条件不难证明△ABE≌△DBC,所以AE=DC,因为DE2+BE2=AE2,BE=CE,所以DE2+CE2=CD2,所以∠DEC=90°,因为∠BEC=60°,所以∠DEB=∠DEC-∠BEC=30°.
试题解析:
(1)证明:如图①中,
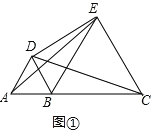
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
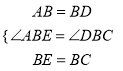 ,
,
∴△ABE≌△DBC,
∴AE=DC;
(2)如图②中,取BE中点F,连接DF,
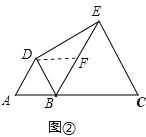
∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,
∴BF=EF=1=BD,∠DBF=60°,
∴△DBF是等边三角形,
∴DF=BF=EF,∠DFB=60°,
∵∠BFD=∠FED+∠FDE,
∴∠FDE=∠FED=30°,
∴∠EDB=180°-∠DBE-∠DEB=90°,
∴DE=![]() ;
;
(3)如图③中,连接DC,
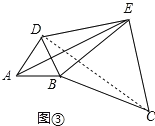
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
 ,
,
-
科目: 来源: 题型:
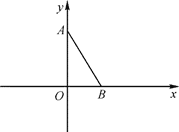
查看答案和解析>>【题目】如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B(
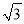 ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”(1)在点 C1 (-2,
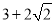 ),点 C2 (0,-2),点 C3 (
),点 C2 (0,-2),点 C3 (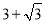 ,
, 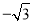 )中,线段 AB 的“等长点”是点______________;
)中,线段 AB 的“等长点”是点______________;(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60,求 m 和 n 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,错误的有( )
A.过两点有且只有一条直线B.直线外一点到这条线段的垂线段叫点到直线的距离
C.两点之间,线段最短D.垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在数轴上画出一条长2019cm的线段AB,则AB盖住的整点个数是( )
A.2019或2020B.2018或2019C.2019D.2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系 xOy 中,点 P 2, 4在( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
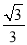 x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=
x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=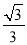 x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)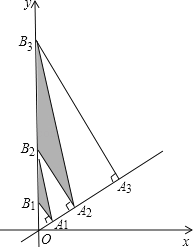
相关试题

