【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)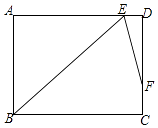
参考答案:
【答案】![]()
【解析】解:延长EF和BC,交于点G
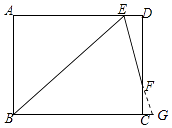
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE= ![]() =
= ![]() ,
,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE= ![]()
由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC
∴ ![]()
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴ ![]() =9+2x+x
=9+2x+x
解得x= ![]()
∴BC=9+2( ![]() ﹣3)=
﹣3)= ![]()
故答案为: ![]()
首先延长EF和BC且延长线交于点G,接下来,再证明三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后再证明三角形BEG为等腰三角形,最后,根据△EFD∽△GFC得出CG与DE的倍数关系,并根据BG=BC+CG进行计算即可.
-
科目: 来源: 题型:
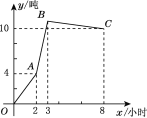
查看答案和解析>>【题目】某仓库有甲、乙、丙三辆运货车,每辆车只负责进货或出货,其中丙车每小时的运输量最多,乙车每小时的运输量最少,且乙车每小时的运输量为6吨.如图是从早晨上班开始库存量y(吨)与时间x(小时)的函数图像,OA段只有甲、丙车工作,AB段只有乙、丙车工作,BC段只有甲、乙车工作.
(1)你能确定甲、乙、丙三辆车哪辆是出货车吗?并说明理由.
(2)若甲、乙、丙三辆车一起工作,一天工作8小时,则仓库的库存量增加多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表
 )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表 ):
):品名
厂家批发价(元/个)
篮球
130
排球
100
(表
 )
)篮球(个)
排球(个)
零售总价(元)
第一天
8
5
1880
第二天
6
10
2160
(表
 )
)请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
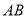 与直线
与直线 交于点
交于点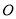 ,
, .小明将一个含
.小明将一个含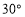 的直角三角板
的直角三角板 如图1所示放置,使顶点
如图1所示放置,使顶点 落在直线
落在直线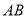 上,过点
上,过点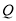 作直线
作直线 交直线
交直线 于点
于点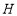 (点
(点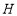 在
在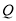 左侧).
左侧).
(1)若
 ,
,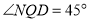 ,则
,则 __________
__________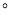 .
.(2)若
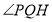 的角平分线交直线
的角平分线交直线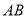 于点
于点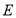 ,如图2.
,如图2.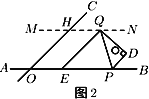

①当
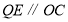 ,
, 时,求证:
时,求证: .
.②小明将三角板保持
 并向左平移,运动过程中,
并向左平移,运动过程中, __________.(用
__________.(用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:①
 ②
② ③
③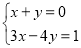 ④
④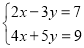 ,比较适宜的方法是( )
,比较适宜的方法是( )A.①②用代入法,③④用加减法B.①③用代入法,②④用加减法
C.②③用代入法,①④用加减法D.②④用代入法,①③用加减法
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).

(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
相关试题

