【题目】探究:
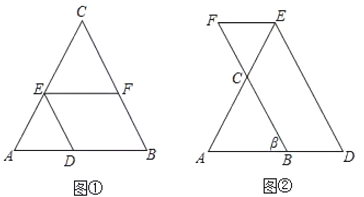
(1)如图①,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的度数.请将下面的解答过程补充完整,并填空.
的度数.请将下面的解答过程补充完整,并填空.
(1)解:
![]() ,
,
![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
![]() ,
,
![]() (___________________________________).
(___________________________________).
![]() (__________________).
(__________________).
![]() .
.
应用:
(2)如图②,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ,若
,若,求
![]() 的大小.(用含
的大小.(用含![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】(1)两直线平行,同位角相等;等量代换;(2)∠DEF=180°-β
【解析】
(1)依据两直线平行,内错角相等以及两直线平行,同位角相等,即可得到∠DEF=∠ABC,进而得出∠DEF的度数.
(2)依据两直线平行,同位角相等以及两直线平行,同旁内角互补,即可得到∠DEF的度数.
(1)∵DE∥BC(已知)
∴∠DEF=∠CFE(两直线平行,内错角相等)
∵EF∥AB
∴∠CFE=∠ABC(两直线平行,同位角相等)
∴∠DEF=∠ABC(等量代换)
∵∠ABC=65°
∴∠DEF=65°
故答案为:两直线平行,同位角相等;等量代换.
(2)∵DE∥BC
∴∠ABC=∠D=β
∵EF∥AB
∴∠D+∠DEF=180°
∴∠DEF=180°-∠D=180°-β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;…,学生发现这些勾股 数的勾都是奇数,且从 3 起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、________、________;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示?小明发现每组第二个数有这样的规律4=
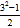 ,12=
,12=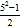 ,24=
,24=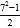 ……,于是他很快表示了第二数为
……,于是他很快表示了第二数为 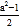 ,则用含a的代数式表示第三个数为________;
,则用含a的代数式表示第三个数为________;(3)用所学知识证明你的结论.
-
科目: 来源: 题型:
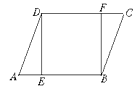
查看答案和解析>>【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8
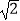 ,则另一直角边AE的长为 .
,则另一直角边AE的长为 . 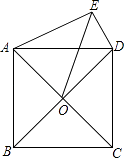
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有个.
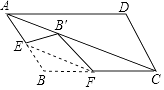
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
相关试题

