【题目】(1)判断下列未知数的值是不是方程2x2+x-1=0的根.
x1=-1,x2=1,x3=![]() .
.
(2)已知m是方程x2-x-2=0的一个根,求代数式m2-m的值.
参考答案:
【答案】(1)x1=-1和x3=![]() 是方程的根;(2)2.
是方程的根;(2)2.
【解析】
(1)利用方程解的定义找到相等关系.即将未知数分别代入方程式看是否成立.
(2)一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值;即用这个数代替未知数所得式子仍然成立;将m代入原方程即可求m2-m的值.
解:(1)当x1=-1时,2x2+x-1=2-1-1=0,所以x1=-11是方程2x2+x-1=0的解;
当x2=1时, 2x2+x-1=2+1-1=2,所以x2=1不是方程2x2+x-1=0的解;
当x3=![]() .时,2x2+x-1=
.时,2x2+x-1=![]() +
+![]() -1=0,所以x3=
-1=0,所以x3=![]() .是方程2x2+x-1=0的解.
.是方程2x2+x-1=0的解.
(2)把x=m代入方程x2-x-2=0可得:m2-m-2=0,
即m2-m=2,
故m2-m的值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.

(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(m-1)x2+(m+1)x+3m-1=0,当m_________时,是一元一次方程;当m_________时,是一元二次方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市上网有两种收费方案,用户可任选其一,A为计时制--1元
 时;B为包月制--80元
时;B为包月制--80元 月,此外每种上网方式都附加通讯费
月,此外每种上网方式都附加通讯费 元
元 时.
时. 某用户每月上网40小时,选哪种方式比较合适?
某用户每月上网40小时,选哪种方式比较合适? 某用户每月有100元钱用于上网,选哪种方式比较合算?
某用户每月有100元钱用于上网,选哪种方式比较合算? 请你设计一个方案,使用户能合理地选择上网方式.
请你设计一个方案,使用户能合理地选择上网方式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是
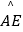 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F. 
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DFDB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列不等式化为“x>a”或“x<a”的形式:
(1)2x>3x-4;
(2)5x-1<14;
(3)-
 x<-3;
x<-3;(4)
 x<
x< x+1.
x+1.
相关试题

