【题目】如图,矩形ABCD中,P为AD上一点,将△ABP沿BP翻折至△EBP,点A与点E重合;
(1)如图1,若AB=10,BC=6,点E落在CD边上,求AP的长;
(2)如图2,若AB=8,BC=6, PE与CD相交于点O,且OE=OD,求AP的长;
(3)如图3,若AB=4,BC=6,点P是AD的中点,求DE的长.

参考答案:
【答案】(1)![]() (2)4.8(3)3.6
(2)4.8(3)3.6
【解析】试题分析:(1)在Rt△BCE中,BC=6,BE=AB=10,根据勾股定理求出CE的值为8,则DE=10-8=2,设AP=x,则PE=x,DP=6-x,在Rt△DPE中,根据勾股定理得出方程,解方程即可;
(2)由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,PE=![]() ,BE=
,BE=![]() ,解得y=
,解得y= ![]() ,再将y=
,再将y= ![]() 代入
代入![]() 中得,x(
中得,x(![]() )=0,所以x=0或x=
)=0,所以x=0或x=![]() ,所以y=
,所以y=![]() ,再根据DE=
,再根据DE=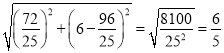 ;
;
试题解析:
(1)∵△ABP沿BP翻折至△EBP,点A与点E重合,AB=10,
∴BE=AB=10,PE=AP,
∴在Rt△BCE中,CE=![]() ,
,
∴DE=CD-CE=2,
设AP=x,则DP=6-x
∵在Rt△DPE中,DP2+DE2=PE2,
∴(6-x)2+22=x2,
∴x=![]() ;
;
(2)∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
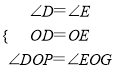
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,
PE=![]() ,BE=
,BE=![]() ,
,
解得y= ![]() ,
,
把y= ![]() 代入
代入![]() 中得,
中得,
x(![]() )=0,
)=0,
所以x=0(舍去)或x=![]() ,
,
所以y=![]() ,
,
∴DE=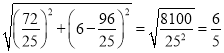 ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )
A.假设a,b,c都是偶数
B.假设a,b,c都不是偶数
C.假设a,b,c至多有一个是偶数
D.假设a,b,c至多有两个是偶数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.

(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,EF//AD,
 =
= .求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
.求证:∠DGA+∠BAC=180°.请将说明过程填写完成.
证明:∵EF//AD,(已知)
∴
 =_____(_____________________________).
=_____(_____________________________).又∵
 =
= (______)
(______)∴
 =
= (________________________).
(________________________).∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2+8x﹣9=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角的度数分别______________________.
相关试题

