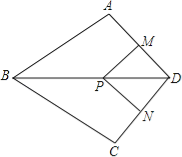
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.

(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
参考答案:
【答案】(1)(2)证明见解析
【解析】试题分析:(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
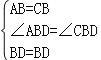 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形的周长是24,相邻两边的长度相差4,那么相邻两边的长分别是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3x=0的根为( )
A. ﹣3 B. 3 C. 0,3 D. 0,﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x﹣y=3,xy=1,则x2+y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2
 ,CD=
,CD= BC,请求出GE的长.
BC,请求出GE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
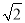 ≈1.4,
≈1.4, 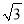 ≈1.7).
≈1.7).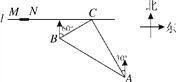
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
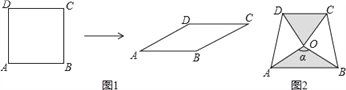
(1)请补全表:
α
30°
45°
60°
90°
120°
135°
150°
S
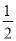
1
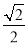
(2)填空:由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=
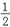 ;当α=135°时,S=S=
;当α=135°时,S=S=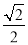 .由上表可以得到S(60°)=S( °);S(30°)=S( °),…,由此可以归纳出S(α)=( °).
.由上表可以得到S(60°)=S( °);S(30°)=S( °),…,由此可以归纳出S(α)=( °).(3)两块相同的等腰直角三角板按图2的方式放置,AD=
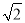 ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
相关试题

