【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
参考答案:
【答案】(1)直拍球拍每副220元,横拍球每副260元;(2)购买直拍球拍30副,则购买横拍球10副时,费用最少.
【解析】
试题分析:(1)设直拍球拍每副x元,横拍球每副y元,根据题意列出二元一次方程组,解方程组即可;
(2)设购买直拍球拍m副,根据题意列出不等式,解不等式求出m的范围,根据题意列出费用关于m的一次函数,根据一次函数的性质解答即可.
试题解析:(1)设直拍球拍每副x元,横拍球每副y元,由题意得:![]() ,解得:
,解得:![]() .
.
答:直拍球拍每副220元,横拍球每副260元;
(2)设购买直拍球拍m副,则购买横拍球(40﹣m)副,由题意得,m≤3(40﹣m),解得,m≤30,设买40副球拍所需的费用为w,则w=(220+20)m+(260+20)(40﹣m)
=﹣40m+11200,∵﹣40<0,∴w随m的增大而减小,∴当m=30时,w取最大值,最大值为﹣40×30+11200=10000(元).
答:购买直拍球拍30副,则购买横拍球10副时,费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题1:在数学课本中我们研究过这样一道题目:如图1,∠ACB=90°,AC=BC,BE⊥MN,AD⊥MN,垂足分别为E、D.图中哪条线段与AD相等?并说明理由. 问题2:试问在这种情况下线段DE、AD、BE具有怎样的等量关系?请写出来,不需要说明理由.
问题3:当直线CE绕点C旋转到图2中直线MN的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并说明理由.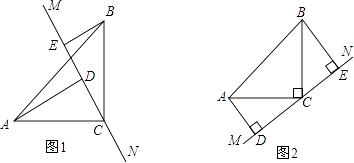
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD、EF相交于点O .
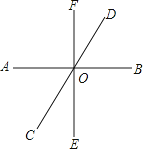
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起,
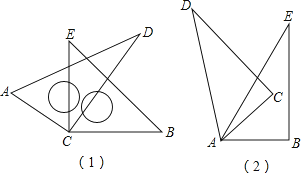
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,则∠DCE=?;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,∠B=4 ∠A,则∠C= ---------------------------( )
A. 18° B. 72° C. 36° D. 144°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )

A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,下列结论中不正确的是--------------------( )
A. 当AB=BC时,它是菱形 B. 当AC=BD时,它是正方形
C. 当∠ABC=90°时,它是矩形 D. 当AC⊥BD时,它是菱形
相关试题

