【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;④∠BDC=∠BAC.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确。
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确。
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°∠ABD,
故③正确;
④∵∠BAC+∠ABC=∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=
∠ABC=![]() ∠ACF,
∠ACF,
∵∠BDC+∠DBC=![]() ∠ACF,
∠ACF,
∴![]() ∠BAC+
∠BAC+![]() ∠ABC=∠BDC+∠DBC,
∠ABC=∠BDC+∠DBC,
∵∠DBC=![]() ∠ABC,
∠ABC,
∴![]() ∠BAC=∠BDC,即∠BDC=
∠BAC=∠BDC,即∠BDC=![]() ∠BAC.
∠BAC.
故④错误。
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,

(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积. -
科目: 来源: 题型:
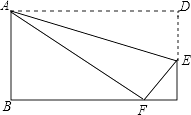
查看答案和解析>>【题目】折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年里约奥运会后,同学们参与体育锻炼的热情高涨,为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下频数分布表和扇形统计图。根据上述信息解答下列问题:

(1)m=____,n=____;
(2)在扇形统计图中,D组所占圆心角的度数是____;
(3)全校共有3000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=9,BC=12,AB=15,点M为AB边上的点,过M作ME⊥AC交AC于E,MF⊥BC交BC于F,连接EF,则EF的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问
(1)有 个小正方体;
(2)有 个小正方体只有两面涂有颜色
(3)有 个小正方体只有3面都涂了颜色.
(4)有 个小正方体6面都未涂色.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元

(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
相关试题

