【题目】如图在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F,
(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积.
参考答案:
【答案】(1)证明见解析(2)16π
【解析】试题分析:(1)连结AD、OD,如图,根据圆周角定理由AB为⊙O的直径得到∠ADB=90°,即AD⊥BC,再根据等腰三角形的性质得BD=CD,则OD为△ABC的中位线,所以OD∥AC,加上EF⊥AC,于是OD⊥EF,然后根据切线的判定定理得EF是⊙O的切线;(2)设⊙O的半径为R,利用OD∥AE得到△FOD∽△FAE,根据相似比可得
![]() =
=![]() ,解得R=4,然后利用圆的面积公式求解.
,解得R=4,然后利用圆的面积公式求解.
试题解析:(1)连结AD、OD,如图,

∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)设⊙O的半径为R,
∵OD∥AE,
∴△FOD∽△FAE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得R=4,
∴⊙O的面积=π42=16π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a-3b=8,那么代数式5+2a-6b的值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3x+6y=9xyB. ﹣a2﹣a2=0
C. 2(3x+2)=6x+2D. ﹣(3x﹣2y)=﹣3x+2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).(1)求抛物线F1所表示的二次函数的表达式及顶点Q的坐标;
(2)在抛物线上是否存在点P,使△BPC的内心在y轴上,若存在,求出点P的坐标,若不存在写出理由;
(3)直线y=kx-6与y轴交于点N,与直线AC的交点为M,当△MNC与△AOC相似时,求点M坐标。

-
科目: 来源: 题型:
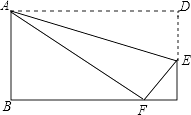
查看答案和解析>>【题目】折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年里约奥运会后,同学们参与体育锻炼的热情高涨,为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下频数分布表和扇形统计图。根据上述信息解答下列问题:

(1)m=____,n=____;
(2)在扇形统计图中,D组所占圆心角的度数是____;
(3)全校共有3000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;④∠BDC=∠BAC.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

