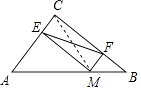
【题目】如图,在△ABC中,AC=9,BC=12,AB=15,点M为AB边上的点,过M作ME⊥AC交AC于E,MF⊥BC交BC于F,连接EF,则EF的最小值为 . 
参考答案:
【答案】![]()
【解析】解:连接CM, 在△ABC中,AC=9,BC=12,AB=15,
∵92+122=152 ,
∴△ABC是直角三角形,
∴∠ACB=90°,
∵ME⊥AC,MF⊥BC,
∴四边形ECFM是矩形,
∴EF=CM,
当CM最小时,则EF最小,根据垂线段最短可知当CM⊥AB时,则CM最小,
∴EF=CM= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了垂线段最短和勾股定理的逆定理的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.
-
科目: 来源: 题型:
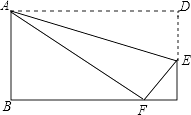
查看答案和解析>>【题目】折叠矩形ABCD,使它的顶点D落在BC边上的F处,如图,AB=6,AD=10,那么CE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年里约奥运会后,同学们参与体育锻炼的热情高涨,为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下频数分布表和扇形统计图。根据上述信息解答下列问题:

(1)m=____,n=____;
(2)在扇形统计图中,D组所占圆心角的度数是____;
(3)全校共有3000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC+∠ABD=90°;④∠BDC=∠BAC.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体的棱分成相等的四份,并做上标记,得到许多小正方体.问
(1)有 个小正方体;
(2)有 个小正方体只有两面涂有颜色
(3)有 个小正方体只有3面都涂了颜色.
(4)有 个小正方体6面都未涂色.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元

(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
相关试题

