【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
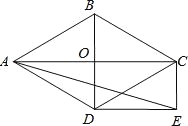
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值.
参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)先证四边形ODEC是平行四边形,然后根据菱形的对角线互相垂直,得到∠DOC=90°,根据矩形的定义即可判定四边形ODEC是矩形;
(2)如图,过点E作EF⊥AD,交AD的延长线于F,构建直角△DEF,在该直角三角形中,∠F=90°,∠EDF=30°,易求DF的长度.所以通过解Rt△AFE来求tan∠EAD的值.
试题解析:(1)∵CE∥BD,DE∥AC,
∴四边形ODEC是平行四边形.
又∵菱形ABCD,
∴AC⊥BD,
∴∠DOC=90°.
∴四边形ODEC是矩形.
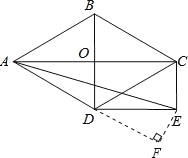
(2)如图,过点E作EF⊥AD,交AD的延长线于F.
∵AC⊥BD,∠ADB=60°,AD=2![]() ,
,
∴OD=![]() ,AO=OC=3.
,AO=OC=3.
∵四边形ODEC是矩形,
∴DE=OC=3,∠ODE=90°.
又∵∠ADO+∠ODE+∠EDF=180°,
∴∠EDF=30°.
在Rt△DEF中,∠F=90°,∠EDF=30°,
∴EF=![]() DE=
DE=![]() .
.
∴DF=![]() .
.
在Rt△AFE中,∠DFE=90°,
∴tan∠EAD=![]() =
=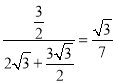 .
.
-
科目: 来源: 题型:
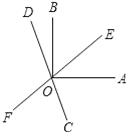
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
-
科目: 来源: 题型:
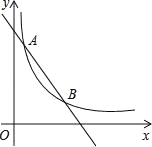
查看答案和解析>>【题目】如图,一次函数y=-x+4的图象与反比例函数y=
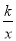 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种药品经过两次降价,药价从原来每盒60元降至到现在48.6元,则平均每次降价的百分比率是
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋子里有5只红球,3只白球,每只球除颜色以外都相同,从中任意摸出1只球,是红球的可能性(选填“大于”“小于”或“等于”)是白球的可能性.
-
科目: 来源: 题型:
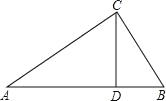
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
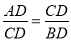 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5,圆心到直线l的距离为4,则直线l与⊙O的位置关系是()
A. 相交 B. 相离 C. 相切 D. 相交或相切
相关试题

