【题目】如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据正方形的性质,易证得AG=EC,∠AGE=∠ECF=135°;再加上(1)得出的相等角,可由ASA判定两个三角形全等;
(2)在Rt△ABE中,根据勾股定理易求得AE2;由(2)的全等三角形知:AE=EF,即△AEF是等腰Rt△,因此其面积为AE2的一半,由此得解.
试题解析:(1)证明:∵G,E分别是正方形ABCD的边AB,BC的中点,∴AG=GB=BE=EC,且∠AGE=180°﹣45°=135°;
又∵CF是∠DCH的平分线,∴∠DCF=∠FCH=45°,∠ECF=90°+45°=135°;
在△AGE和△ECF中,∵AG=EC,∠AGE=∠ECF=135°,∠GAE=∠FEC;
∴△AGE≌△ECF;
(2)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,∴BE=![]() BC=
BC=![]() AB=
AB=![]() a,根据勾股定理得:AE=
a,根据勾股定理得:AE=![]() =
=![]() a,∴S△AEF=
a,∴S△AEF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
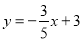 与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
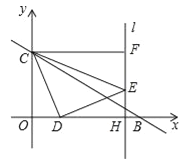
与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个整数96666…0用科学记数法表示为9.6666×109,则原数中“0“的个数为( )
A.4B.5C.6D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ab=﹣5,a﹣b=6,则a2+b2=( )
A.13
B.19
C.26
D.37 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)
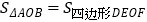 中正确的有( )
中正确的有( )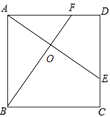
A. 4个
B. 3个
C. 2个
D. 1个 -
科目: 来源: 题型:
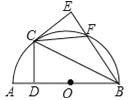
查看答案和解析>>【题目】如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
(1)判断CE与半圆O的位置关系,并给予证明.
(2)点C在运动时,四边形OCFB的形状可变为菱形吗?若可以,猜想此时∠AOC的大小,并证明你的结论;若不可以,请说明理由.
-
科目: 来源: 题型:
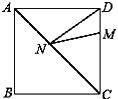
查看答案和解析>>【题目】如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是 .
相关试题

