【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
求证:(1)BD平分∠ABC;
(2)△BCD为等腰三角形.

参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由AB的中垂线MN交AC于点D,交AB于M,求得△ABD是等腰三角形,即可求得∠ABD的度数,然后根据等边对等角,求得∠DBC的度数,从而得证;
(2)根据(1)的结论和外角的性质,可得∠BDC=∠C,再根据等角对等边得证.
试题解析:(1)∵MN为AB的中垂线,
∴AD=BD,
则∠A=∠ABD=36°,
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∴∠DBC=36°,
因此,BD平分∠ABC;
(2)由①和∠2=36° ∠C=72° ,
∵∠BDC=180°-36°-72°=72°,
∴∠C=∠ABD+∠DBC=∠BDC,
∴△BCD为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a与5的和的3倍用代数式表示是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
证明:∵∠C=∠1,∠D=∠2(已知)
又∵∠1=∠2( )
∴ ( )
∴AC∥BD( )
∴ (两直线平行,内错角相等)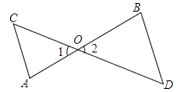
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题:
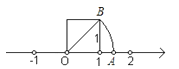
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.
(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+3x+5的值为7,则代数式3x2+9x﹣2的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示.
(1)建立适当的平面直角坐标系,使医院的坐标为(3,0)并写出小明家、学校、游乐场的坐标;
(2)根据蜀河大坝蓄水工程需要,小明家及学校、医院、游乐场需要等距离整体迁移,已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示,且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到,请先在图中描出A、B、C、D的位置,画出四边形ABCD,
然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数
 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.(1)求一次函数y1=k1x+b与反比例函数
 的解析式;
的解析式;(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.

相关试题

