【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?
参考答案:
【答案】
(1)解:设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得40x+30(20﹣x)=650,
解得x=5,
则20﹣x=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)解:设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得 ![]() ,解得
,解得 ![]() ≤x≤8,
≤x≤8,
∵x为整数,
∴x=7或x=8,
当x=7时,20﹣x=13;当x=8时,20﹣x=12;
答:该公司有2种不同的购买方案:甲种奖品购买了:7件,乙种奖品购买了13件或甲种奖品购买了8件,乙种奖品购买了12件.
【解析】(1)设出未知数x,由“共花费了650元“列出方程40x+30(20﹣x)=650即可;(2)设甲种奖品购买了x件, 分别用x 的代数式表达出“购买乙种奖品的件数不超过甲种奖品件数的2倍”和“总花费不超过680”,构建不等式组,取整数解.
【考点精析】利用一元一次不等式组的应用对题目进行判断即可得到答案,需要熟知1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.

-
科目: 来源: 题型:
查看答案和解析>>【题目】受寒潮影响,淘宝网上的电热取暖器销售火旺,某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一天
3台
5台
1800元
第二天
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的电热取暖器的销售单价;
(2)若电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,求A种型号的电热取暖器最多能采购多少台? -
科目: 来源: 题型:
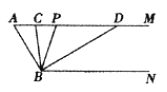
查看答案和解析>>【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D

(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=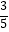 ,求AC和CD的长.
,求AC和CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+4与反比例函数y=
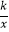 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点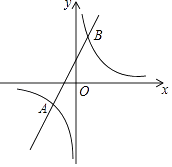
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式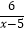 >x的解集.
>x的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;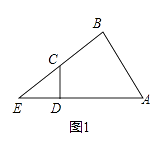
(2)如图2,若∠ABC=120°,cos∠ADC= ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;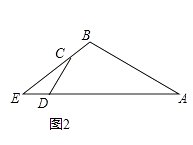
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
相关试题

