【题目】如图,直线y=2x+4与反比例函数y= ![]() 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点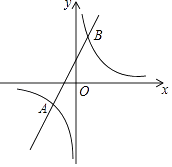
(1)求k的值;
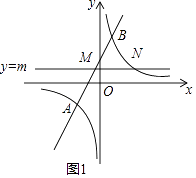
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式 ![]() >x的解集.
>x的解集.
参考答案:
【答案】
(1)∵点A(﹣3,a)在y=2x+4与y= ![]() 的图象上,
的图象上,
∴2×(﹣3)+4=a,
∴a=﹣2,
∴k=(﹣3)×(﹣2)=6;
(2)∵M在直线AB上,
∴M( ![]() ,m),N在反比例函数y=
,m),N在反比例函数y= ![]() 上,
上,
∴N( ![]() ,m),
,m),
∴MN=xN﹣xM= ![]() ﹣
﹣ ![]() =4或xM﹣xN=
=4或xM﹣xN= ![]() ﹣
﹣ ![]() =4,
=4,
解得:∵m>0,
∴m=2或m=6+4 ![]() ;
;
(3)x<﹣1或5<x<6,
由 ![]() >x得:
>x得: ![]() ﹣x>0,
﹣x>0,
∴ ![]() >0,
>0,
∴ ![]() <0,
<0,
∴ ![]() 或
或 ![]() ,
,
结合抛物线y=x2﹣5x﹣6的图象可知,由 ![]() 得
得
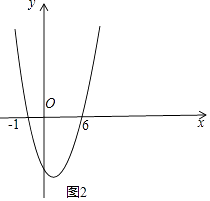
![]() ,
,
∴ ![]() 或
或 ![]() ,
,
∴此时x<﹣1,
由 ![]() 得,
得, ![]() ,
,
∴ ![]() ,
,
解得:5<x<6,
综上,原不等式的解集是:x<﹣1或5<x<6.
【解析】(1)把点A(﹣3,a)分别代入y=2x+4与y=![]() 中,即可求出k;(2)由M、N点均在双曲线上,用m的代数式表示两点坐标,根据MN=4,即
中,即可求出k;(2)由M、N点均在双曲线上,用m的代数式表示两点坐标,根据MN=4,即
xN-xM=4,建立方程求出m;(3)变形不等式![]() ,即
,即![]() ,分两种情况讨论:
,分两种情况讨论:![]() 或
或![]() ,运用数形结合的思想,画出y=
,运用数形结合的思想,画出y=![]() 的图象,找出与x轴交点的横坐标,即可求出.
的图象,找出与x轴交点的横坐标,即可求出.
-
科目: 来源: 题型:
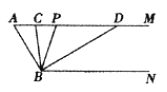
查看答案和解析>>【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D

(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=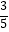 ,求AC和CD的长.
,求AC和CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;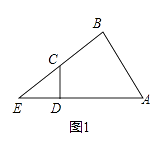
(2)如图2,若∠ABC=120°,cos∠ADC= ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;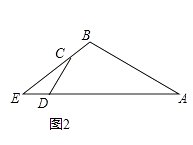
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.

(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,AB与CD有怎样的位置关系?并说明理由.

相关试题

