【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.

参考答案:
【答案】(1)证明见解析;(2)四边形AECF是菱形;理由见解析
【解析】
(1)由已知条件得出AB=AO,AC=AG,由SAS证明△ABC≌△AOG即可;
(2)由矩形的性质得出∠ABC=90°,AD∥BC,得出∠OAF=∠OCE,由ASA证明△AOF≌△COE,得出OF=OE,得出四边形AECF是平行四边形,再由全等三角形的对应角相等得出∠AOG=∠ABC=90°,即可得出结论.
(1)证明:∵点O是AC的中点,
∴AO=CO=![]() AC,
AC,
∵AC=2AB,BG=AB,
∴AB=AO,AC=AG,
在△ABC和△AOG中, ,
,
∴△ABC≌△AOG(SAS);
(2)四边形AECF是菱形;理由如下:
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中, ,
,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
∵△ABC≌△AOG,
∴∠AOG=∠ABC=90°,
∴AC⊥EF,
∴四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相较于点O,OE⊥AB与点O,OB平分∠DOF,∠DOE=62°.
求∠AOC、∠EOF、∠COF的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )

A. 112.5° B. 125° C. 135° D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
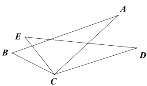
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】受寒潮影响,淘宝网上的电热取暖器销售火旺,某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一天
3台
5台
1800元
第二天
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的电热取暖器的销售单价;
(2)若电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,求A种型号的电热取暖器最多能采购多少台? -
科目: 来源: 题型:
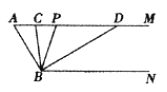
查看答案和解析>>【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?
相关试题

