【题目】已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图1,若∠ABC=∠ADC=90°,求证:EDEA=ECEB;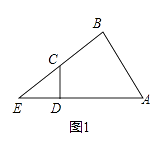
(2)如图2,若∠ABC=120°,cos∠ADC= ![]() ,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;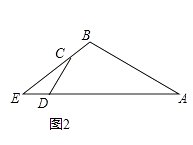
(3)如图3,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC= ![]() ,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示)
参考答案:
【答案】
(1)解:如图1中,
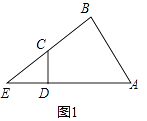
∵∠ADC=90°,∠EDC+∠ADC=180°,
∴∠EDC=90°,
∵∠ABC=90°,
∴∠EDC=∠ABC,
∵∠E=∠E,
∴△EDC∽△EBA,
∴ ![]() =
= ![]() ,
,
∴EDEA=ECEB.
(2)解:如图2中,过C作CF⊥AD于F,AG⊥EB于G.
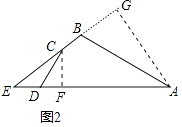
在Rt△CDF中,cos∠ADC= ![]() ,
,
∴ ![]() =
= ![]() ,∵CD=5,
,∵CD=5,
∴DF=3,
∴CF= ![]() =4,
=4,
∵S△CDE=6,
∴ ![]() EDCF=6,
EDCF=6,
∴ED= ![]() =3,EF=ED+DF=6,
=3,EF=ED+DF=6,
∵∠ABC=120°,∠G=90°,∠G+∠BAG=∠ABC,
∴∠BAG=30°,
∴在Rt△ABG中,BG= ![]() AB=6,AG=
AB=6,AG= ![]() =6
=6 ![]() ,
,
∵CF⊥AD,AG⊥EB,
∴∠EFC=∠G=90°,∵∠E=∠E,
∴△EFC∽△EGA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EG=9 ![]() ,
,
∴BE=EG﹣BG=9 ![]() ﹣6,
﹣6,
∴S四边形ABCD=S△ABE﹣S△CDE= ![]() (9
(9 ![]() ﹣6)×6
﹣6)×6 ![]() ﹣6=75﹣18
﹣6=75﹣18 ![]() .
.
(3)解:如图3中,作CH⊥AD于H,则CH=4,DH=3,

∴tan∠E= ![]() ,
,
作AG⊥DF于点G,设AD=5a,则DG=3a,AG=4a,
∴FG=DF﹣DG=5+n﹣3a,
∵CH⊥AD,AG⊥DF,∠E=∠F,
易证△AFG∽△CEH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
∴AD=5a= ![]() .
.
【解析】要证乘积式等式成立,可化为比例式即![]() 成立,进一步确定三角形△EDC与△EBA相似;(2)特殊角、三角函数应放在直角三角形中运用,因此需作垂线构造直角三角形,恰好构造出第(1)题的图形,借鉴第一问的思路,求出EG,进一步利用面积之差,求出四边形ABCD的面积.(3)作垂线构造出直角三角形,利用相似三角形△AFG∽△CEH,构建比例式,求出AD的长.
成立,进一步确定三角形△EDC与△EBA相似;(2)特殊角、三角函数应放在直角三角形中运用,因此需作垂线构造直角三角形,恰好构造出第(1)题的图形,借鉴第一问的思路,求出EG,进一步利用面积之差,求出四边形ABCD的面积.(3)作垂线构造出直角三角形,利用相似三角形△AFG∽△CEH,构建比例式,求出AD的长.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方),还要掌握锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D

(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=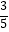 ,求AC和CD的长.
,求AC和CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+4与反比例函数y=
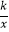 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点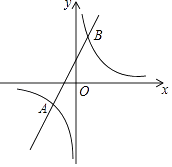
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式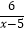 >x的解集.
>x的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.

(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、F在线段AB上,点E、G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,AB与CD有怎样的位置关系?并说明理由.

相关试题

