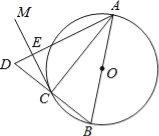
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD=BC,连接AD与CM交于点E,若⊙O的半径为2,ED=1,求AC的长.
参考答案:
【答案】(1)证明参见解析;(2)2![]() .
.
【解析】
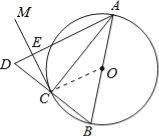
试题分析:(1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,得出结论,(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC.
试题解析:(1)连接OC.∵AB为⊙O的直径,∴∠ACB=90°.∴∠ABC+∠BAC=90°.∵CM是⊙O的切线,∴OC⊥CM.∴∠ACM+∠ACO=90°.∵CO=AO,∴∠BAC=∠ACO.∴∠ACM=∠ABC.(2)∵BC=CD,OB=OA,∴OC∥AD.又∵OC⊥CE,∴CE⊥AD,∵∠ACD=∠ACB=90°,∴∠AEC=∠ACD.∴△ADC∽△ACE.∴![]() .∵⊙O的半径为2,∴AD=4.∴
.∵⊙O的半径为2,∴AD=4.∴![]() .∴AC=2
.∴AC=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为4的菱形ABCD中,AC为其对角线,∠ABC=60°点M、N是分别是边BC、边CD上的动点,且MB=NC.连接AM、AN、MN.MN交AC于点P.
(1)△AMN是什么特殊的三角形?说明理由.并求其面积最小值;
(2)求点P到直线CD距离的最大值;
(3)如图2,已知MB=NC=1,点E、F分别是边AM、边AN上的动点,连接EF、PF,EF+PF是否存在最小值?若存在,求出最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2-2x+m=0有两个不相等的实数根.请你写出一个满足条件的m值:m=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x3y2﹣x3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣1=0的根为( )
A.x=1
B.x=﹣1
C.x1=1,x2=﹣1
D.x1=0,x2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)3等于( )
A.﹣9
B.9
C.﹣27
D.27 -
科目: 来源: 题型:
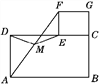
查看答案和解析>>【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
① ②
②
相关试题

