【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
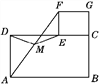 ①
① ②
②
参考答案:
【答案】猜想与证明:猜想DM与ME的数量关系是:DM=ME. 拓展与延伸:DM=ME,DM⊥ME
【解析】试题分析:猜想:延长EM交AD于点H,利用△FME≌△AMH,得出HM=EM,再利用直角三角形中,斜边的中线等于斜边的一半证明.
(1)延长EM交AD于点H,利用△FME≌△AMH,得出HM=EM,再利用直角三角形中,斜边的中线等于斜边的一半证明,
(2)连接AE,AE和EC在同一条直线上,再利用直角三角形中,斜边的中线等于斜边的一半证明,
试题解析:猜想:DM=ME
证明:如图1,延长EM交AD于点H,
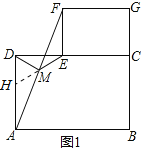
∵四边形ABCD和CEFG是矩形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,
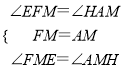
∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM,
∴DM=HM=ME,
∴DM=ME.
(1)如图1,延长EM交AD于点H,
∵四边形ABCD和CEFG是正方形,
∴AD∥EF,
∴∠EFM=∠HAM,
又∵∠FME=∠AMH,FM=AM,
在△FME和△AMH中,

∴△FME≌△AMH(ASA)
∴HM=EM,
在RT△HDE中,HM=EM,
∴DM=HM=ME,
∴DM=ME.
∵四边形ABCD和CEFG是正方形,
∴AD=CD,CE=CF,
∵△FME≌△AMH,
∴EF=AH,
∴DH=DE,
∴△DEH是等腰直角三角形,
又∵MH=ME,
(2)如图2,连接AE,
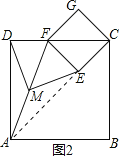
∵四边形ABCD和ECGF是正方形,
∴∠FCE=45°,∠FCA=45°,
∴AE和EC在同一条直线上,
在Rt△ADF中,AM=MF,
∴DM=AM=MF,∠MDA=∠MAD,
∴∠DMF=2∠DAM.
在Rt△AEF中,AM=MF,
∴AM=MF=ME,
∴DM=ME.
∵∠MDA=∠MAD,∠MAE=∠MEA,
∴∠DME=∠DMF+∠FME=∠MDA+∠MAD+∠MAE+∠MEA=2(∠DAM+∠MAE)=2∠DAC=2×45°=90°.
∴DM⊥ME.
-
科目: 来源: 题型:
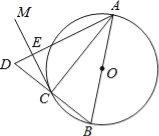
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使CD=BC,连接AD与CM交于点E,若⊙O的半径为2,ED=1,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣1=0的根为( )
A.x=1
B.x=﹣1
C.x1=1,x2=﹣1
D.x1=0,x2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)3等于( )
A.﹣9
B.9
C.﹣27
D.27 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a3+a3=a6B. (﹣a2)3=a6C. a5÷a﹣2=a7D. (a+1)0=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】一群小孩分一堆苹果,1人3个多7个,1人4个少3个,则有_____ 个小孩,_____个苹果.
-
科目: 来源: 题型:
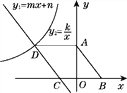
查看答案和解析>>【题目】如图,在菱形ABCD中,AD∥x轴,点A的坐标为(0,4),点B的坐标为(3,0).CD边所在直线y1=mx+n与x轴交于点C,与双曲线y2=
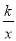 (x<0)交于点D.
(x<0)交于点D.(1)求直线CD对应的函数表达式及k的值.
(2)把菱形ABCD沿y轴的正方向平移多少个单位后,点C落在双曲线y2=
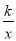 (x<0)上?
(x<0)上?(3)直接写出使y1>y2的自变量x的取值范围.
相关试题

