【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
参考答案:
【答案】(1)是;(2)4或6或8;(3)详见解析.
【解析】试题分析:(1)由“巧点”定义即可判断;
(2)分BC=2AC、BC=AC、BC=![]() AC三种情况讨论即可;
AC三种情况讨论即可;
(3)分P为A、Q的巧点时和Q为A、P的巧点时两种情况讨论即可.
试题解析:(1)
![]()
是 ;
(2)①如图:
![]()
当BC=2AC时,AC=![]() ×12=4cm;
×12=4cm;
②如图:
![]()
当BC=AC时,AC=![]() ×12=6cm;
×12=6cm;
③如图:
![]()
当BC=![]() AC时,AC=
AC时,AC=![]() ×12=8cm;
×12=8cm;
故BC长为4cm或6cm或8cm;
4或6或8;
(3)t秒后,AP=2t,AQ=12-2t(![]() )
)
①由题意可知A不可能为P、Q两点的巧点,此情况排除;
②当P为A、Q的巧点时,
Ⅰ. AP=![]() AQ 即
AQ 即![]() 得
得![]() s
s
Ⅱ. AP=![]() AQ即
AQ即![]() 得
得![]() s
s
Ⅲ. AP=![]() AQ即
AQ即![]() 得
得![]() s
s
③当Q为A、P的巧点时
Ⅰ. AQ=![]() AP 即
AP 即![]() 得
得
Ⅱ. AQ=![]() AP即
AP即![]() 得
得![]() s
s
Ⅲ. AQ=![]() AP即
AP即![]() 得
得![]() s
s
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
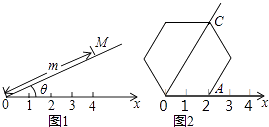
A.(60°,4)
B.(45°,4)
C.(60°,2 )
)
D.(50°,2 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗的数量应满足怎样的条件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
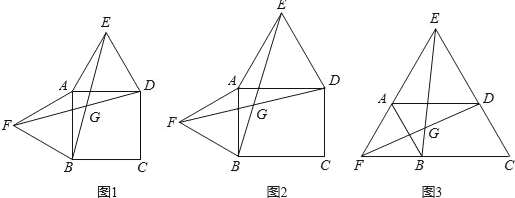
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
①a=40,m=1;
②乙的速度是80km/h;
③甲比乙迟 h到达B地;
h到达B地;
④乙车行驶 小时或
小时或  小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=
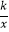 (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 . 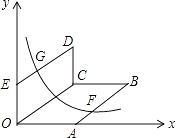
-
科目: 来源: 题型:
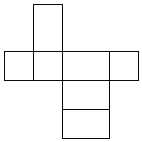
查看答案和解析>>【题目】如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为3 cm,长方形的长为5 cm,宽为3 cm,请直接写出修正后所折叠而成的长方体的体积是 cm3.
相关试题

