【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论: ⑴b2﹣4ac>0;
⑵2a=b;
⑶点(﹣ ![]() ,y1)、(﹣
,y1)、(﹣ ![]() ,y2)、(
,y2)、( ![]() ,y3)是该抛物线上的点,则y1<y2<y3;
,y3)是该抛物线上的点,则y1<y2<y3;
⑷3b+2c<0;
⑸t(at+b)≤a﹣b(t为任意实数).
其中正确结论的个数是( )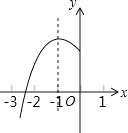
A.2
B.3
C.4
D.5
参考答案:
【答案】C
【解析】解:(1)由函数图象可知,抛物线与x轴有两个不同的交点,
∴关于x的方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2﹣4ac>0,
∴(1)正确;(2)∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,
∴﹣ ![]() =﹣1,
=﹣1,
∴2a=b,
∴(2)正确;(3)∵抛物线的对称轴为x=﹣1,点( ![]() ,y3)在抛物线上,
,y3)在抛物线上,
∴(﹣ ![]() ,y3).
,y3).
∵﹣ ![]() <﹣
<﹣ ![]() <﹣
<﹣ ![]() ,且抛物线对称轴左边图象y值随x的增大而增大,
,且抛物线对称轴左边图象y值随x的增大而增大,
∴y1<y3<y2.
∴(3)错误;(4)∵当x=﹣3时,y=9a﹣3b+c<0,且b=2a,
∴9a﹣3×2a+c=3a+c<0,
∴6a+2c=3b+2c<0,
∴(4)正确;(5)∵b=2a,
∴方程at2+bt+a=0中△=b2﹣4aa=0,
∴抛物线y=at2+bt+a与x轴只有一个交点,
∵图中抛物线开口向下,
∴a<0,
∴y=at2+bt+a≤0,
即at2+bt≤﹣a=a﹣b.
∴(5)正确.
故选C.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c),以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=
 (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.解:猜想: .
证明:

-
科目: 来源: 题型:
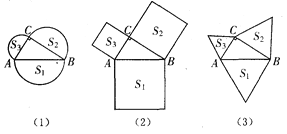
查看答案和解析>>【题目】如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3。(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则
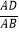 的值为( )
的值为( ) 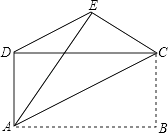
A.
B.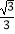
C.
D.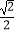
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2﹣12x+k=0的两个根,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程
 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?经过独立思考与分析后,小明和小聪开始交流解题思路如下:
小明说:解这个关于x的分式方程,得到方程的解为
 .由题意可得
.由题意可得 ,所以
,所以 ,问题解决.
,问题解决.小聪说:你考虑的不全面.还必须保证
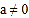 才行.
才行.请回答:_______________的说法是正确的,并说明正确的理由是:__________________.
完成下列问题:
(1)已知关于x的方程
 的解为非负数,求m的取值范围;
的解为非负数,求m的取值范围;(2)若关于x的分式方程
 无解.直接写出n的取值范围.
无解.直接写出n的取值范围.
相关试题

