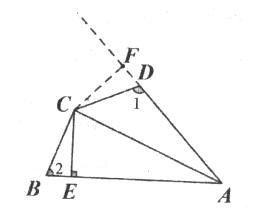
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

参考答案:
【答案】∠1+∠2=180°
【解析】
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件![]() ,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
猜想:∠1+∠2=180°
证明:过C点作CF⊥AD延长线于点F,
∵CE⊥AB,AC平分∠DAB,
∴CB=CF,
∠CEB=∠CFD=90°,
在Rt△CEA和Rt△CFA中
∵![]()
∴Rt△CEA≌Rt△CFA(HL),
∴AE=AF,
∵![]() ,
,
AE+AF=AF-FD+AE+BE,
∴FD=BE,
在△CEB和△CFD中
∵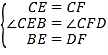
∴△CEB≌△CFD(SAS),
∴∠2=∠CDF,
∵∠CDF+∠1=180°,
∴∠1+∠2=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如:
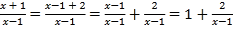 ;
; 
(1)下列分式中,属于真分式的是:________(填序号);
①
 ②
② ③
③ ④
④
(2)将假分式
 化成整式与真分式的和的形式:
化成整式与真分式的和的形式:  =________+________;
=________+________;(3)将假分式
 化成整式与真分式的和的形式:
化成整式与真分式的和的形式:  =__________________.
=__________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC',△AEB≌△AEB',且C'D∥EB'∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是_____°.(用含x的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

-
科目: 来源: 题型:
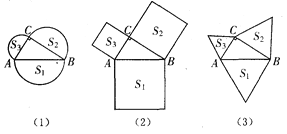
查看答案和解析>>【题目】如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3。(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则
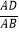 的值为( )
的值为( ) 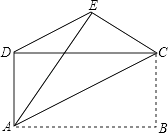
A.
B.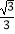
C.
D.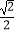
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论: ⑴b2﹣4ac>0;
⑵2a=b;
⑶点(﹣ ,y1)、(﹣
,y1)、(﹣  ,y2)、(
,y2)、(  ,y3)是该抛物线上的点,则y1<y2<y3;
,y3)是该抛物线上的点,则y1<y2<y3;
⑷3b+2c<0;
⑸t(at+b)≤a﹣b(t为任意实数).
其中正确结论的个数是( )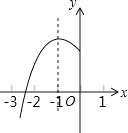
A.2
B.3
C.4
D.5
相关试题

