【题目】(1)已知∠AOB=25°42′,则∠AOB的余角为 ,∠AOB的补角为 ;
(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;
(3)如图,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,且∠AOB=25°,则经过多少时间后,△AOB的面积第一次达到最大值.

参考答案:
【答案】(1)64°18′,154°18′;(2)∠MON=![]() ;(3)
;(3)![]() 分
分
【解析】
(1)依据余角和补角的定义即可求出∠AOB的余角和补角;
(2)依据角平分线的定义表示出∠AOM=∠BOM=![]() ∠AOB=
∠AOB=![]() α,∠CON=∠BON=
α,∠CON=∠BON=![]() ∠COB=
∠COB=![]() β,最后再依据∠MON与这些角的关系求解即可;(3)当OA⊥OB时面积最大,此时∠AOB=90°,根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.
β,最后再依据∠MON与这些角的关系求解即可;(3)当OA⊥OB时面积最大,此时∠AOB=90°,根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.
解:(1)∵∠AOB=25°42',
∴∠AOB的余角=90°﹣25°42'=64°18′,
∠AOB的补角=180°﹣25°42'=154°18′;
故答案为:64°18′,154°18′;
(2)
①如图1:
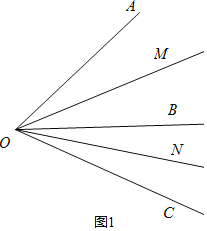
∵∠AOB=α,∠BOC=β
∴∠AOC=∠AOB+∠BOC=90°+30°=120°
∵OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=![]() ∠AOB=
∠AOB=![]() α,∠CON=∠BON=
α,∠CON=∠BON=![]() ∠COB=
∠COB=![]() β,
β,
∴∠MON=∠BOM+∠CON=![]() ;
;
②如图2,

∠MON=∠BOM﹣∠BON=![]() ;
;
③如图3,

∠MON=∠BON﹣∠BOM=![]() .
.
∴∠MON为![]() 或
或![]() 或
或![]() .
.
(3)当OA⊥OB时,△AOB的面积第一次达到最大值,此时∠AOB=90°,
设经过x分钟后,△AOB的面积第一次达到最大值,
根据题意得:6x+25﹣![]() ×30=90,
×30=90,
解得x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
-
科目: 来源: 题型:
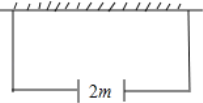
查看答案和解析>>【题目】如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
(1)若墙长为18m,要围成养鸡场的面积为150m2,则养鸡场的长和宽各为多少?
(2)围成养鸡场的面积能否达到200m2?请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A是双曲线
 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点
 如图,直线
如图,直线 和反比例函数
和反比例函数 的图象交于
的图象交于 两点,则落在图中阴影部分
两点,则落在图中阴影部分 不包含边界
不包含边界 内的整点个数有
内的整点个数有 个.
个.
A. 2
B. 3
C. 4
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.

-
科目: 来源: 题型:
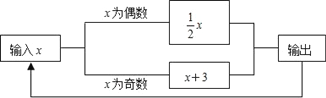
查看答案和解析>>【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
相关试题

