搜索
【题目】制作一种产品，需先将材料加热达到60 ℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（min）．据了解，当该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加热前的温度为15 ℃，加热5分钟后温度达到60 ℃．
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低于15 ℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？
参考答案：
【答案】（1）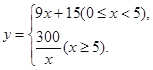
（2）20分钟
【解析】解：（1）材料加热时，设y=ax+15（a≠0），
由题意得60=5a+15，
解得a=9，
则材料加热时，y与x的函数关系式为y=9x+15（0≤x≤5）．
停止加热时，设y=（k≠0），
由题意得60=，
解得k=300，
则停止加热进行操作时y与x的函数关系式为y=
（x≥5）；
（2）把y=15代入y=，得x=20，
因此从开始加热到停止操作，共经历了20分钟．
答：从开始加热到停止操作，共经历了20分钟．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某开发公司生产的960件新产品需要精加工后才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的
，甲、乙两个工厂每天各能加工多少个新产品? -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
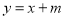与双曲线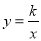
相交于A（2，1）、B两点．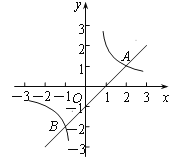
（1）求m及k的值；
（2）不解关于x、y的方程组
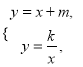直接写出点B的坐标；（3）直线
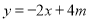经过点B吗？请说明理由．【答案】（1）m=－1，k=2；（2）（－1，－2）；（3）经过
【解析】试题分析：（1）把A（2，1）分别代入直线
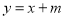与双曲线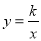
即可求得结果；（2）根据函数图象的特征写出两个图象的交点坐标即可；
（3）把x=－1，m=－1代入
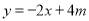即可求得y的值，从而作出判断.（1）把A（2，1）分别代入直线
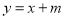与双曲线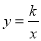
的解析式得m=－1，k=2；（2）由题意得B的坐标（－1，－2）；
（3）当x=－1，m=－1代入
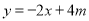得y=－2×(－1)+4×(－1)=2－4=－2所以直线
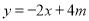经过点B(－1，－2).考点：反比例函数的性质
点评：反比例函数的性质是初中数学的重点，是中考常见题，一般难度不大，需熟练掌握.
【题型】解答题
【结束】
20【题目】某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数，其图象如图所示(千帕是一种压强单位)
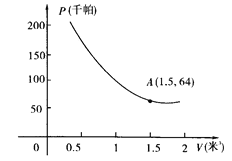
（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时，气球内的气压是多少千帕；
（3）当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。
-
科目： 来源： 题型：
查看答案和解析>>【题目】位于张家界核心景区的贺龙铜像，是我国近百年来最大的铜像．铜像由像体AD和底座CD两部分组成．如图，在Rt△ABC中，∠ABC=70.5°，在Rt△DBC中，∠DBC=45°，且CD=2.3米，求像体AD的高度（最后结果精确到0.1米，参考数据：sin70.5°≈0.943，cos70.5°≈0.334，tan70.5°≈2.824）
-
科目： 来源： 题型：
查看答案和解析>>【题目】公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数
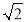，导致了第一次数学危机.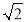是无理数的证明如下：假设
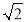是有理数，那么它可以表示成
（
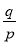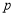与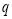
是互质的两个正整数）.于是
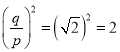，所以，
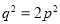.于是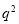
是偶数，进而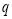是偶数.从而可设
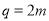，所以
，
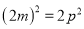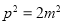，于是可得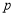也是偶数.这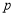与“与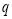是互质的两个正整数”矛盾，从而可知“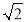是有理数”的假设不成立，所以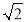，是无理数.这种证明“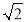是无理数”的方法是( )A.综合法B.反证法C.举反例法D.数学归纳法
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：
①4ac＜b2；
②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；
③3a+c＞0
④当y＞0时，x的取值范围是﹣1≤x＜3
⑤当x＜0时，y随x增大而增大
其中结论正确的个数是（ ）
A.4个
B.3个
C.2个
D.1个 -
科目： 来源： 题型：
查看答案和解析>>【题目】某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图)，已知装修旧墙壁的费用为20元/m2，新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m，一面旧墙壁AB的长为x m，修建健身房墙壁的总投入为y元.
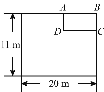
(1)求y与x的函数关系式；
(2)为了合理利用大厅，要求自变量x必须满足条件:8≤x≤12，当投入的资金为4800元时，问利用旧墙壁的总长度为多少?
相关试题
