【题目】如图,正方形ABCD的边长为2 ![]() ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为 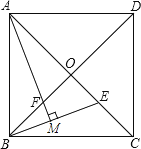
参考答案:
【答案】![]()
【解析】解:∵正方形ABCD
∴AO=BO,∠AOF=∠BOE=90°
∵AM⊥BE,∠AFO=∠BFM
∴∠FAO=∠EBO
在△AFO和△BEO中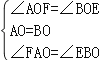
∴△AFO≌△BEO(ASA)
∴FO=EO
∵正方形ABCD的边长为2 ![]() ,E是OC的中点
,E是OC的中点
∴FO=EO=1=BF,BO=2
∴直角三角形BOE中,BE= ![]() =
= ![]()
由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO
∴ ![]() ,即
,即 ![]() ∴FM=
∴FM= ![]() 所以答案是:
所以答案是: ![]()
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
有一些相同的房间需要粉刷,一天 3名一级技工去粉刷 8个房间,结果其中有 50
 墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40
墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40 墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10
墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10 墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?
墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知 P是线段 AB上的一点,
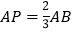 ,C, D两点从 A, P同时出发,分别以2
,C, D两点从 A, P同时出发,分别以2 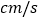 ,1
,1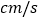 的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=
的速度沿 AB方向运动,当点 D到达终点 B时,点C也停止运动,设AB=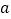
 ,点 C,D的运动时间为
,点 C,D的运动时间为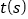 .
.(1)用含
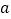 和 的代数式表示线段 CP 的长度.
和 的代数式表示线段 CP 的长度.(2)当 t =5时,
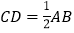 ,求线段 AB的长.
,求线段 AB的长.(3)当 BC-AC=PC时,求
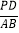 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上,点 A 的初始位置表示的数为 1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第 2 次从点 A1 向右移动 6 个单位长度至点 A2,第 3 次从点 A2 向左移动 9 个单位长度至点 A3,…,按照这种移动方式进行下去,点 A4 表示的数,是__________ ,如果点 An 与原点的距离不小于 20, 那么 n 的最小值是________________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B、游两个景区;C、游一个景区;D、不到这三个景区游玩.现根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题:
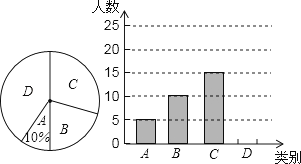
(1)八(1)班共有学生人,在扇形统计图中,表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成下列题目.
 求:
求: 的值.
的值.对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成
 的形式,而
的形式,而 ,这样就把
,这样就把 一项
一项 分
分 裂成了两项.
裂成了两项.试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出
 的值.
的值. 若
若
 求:A、B的值:
求:A、B的值: 求:
求: 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD、DEFG都是正方形,AB与CG交于点
 下列结论:
下列结论: ;
; ;
; ;
; ;
; 其中正确的有______;
其中正确的有______;
相关试题

