【题目】如图,在四边形ABCD中,∠B=90°,AB∥ED ,交BC于E,交 AC于F, DE = BC,![]() .
.

(1) 求证:△FCD 是等腰三角形
(2) 若AB=3.5cm,求CD的长。
参考答案:
【答案】(1)详见解析;(2)CD=7cm.
【解析】
(1)首先根据平行线的性质得出∠DEC=∠B=90°,然后在△DCE中根据三角形内角和定理得出∠DCE的度数,从而得出∠DCF的度数.在△CDF中根据等角对等边证明出△FCD是等腰三角形;
(2)先证明△ACB≌△CDE,得出AC=CD,再根据含30°角的直角三角形的性质求解即可.
(1)∵DE∥AB,∠B=90°,∴∠DEC=90°,∴∠DCE=90°﹣∠CDE=60°,∴∠DCF=∠DCE﹣∠ACB=30°,∴∠CDE=∠DCF,∴DF=CF,∴△FCD是等腰三角形;
(2)在△ACB和△CDE中,∵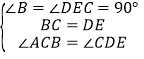 ,∴△ACB≌△CDE,∴AC=CD.
,∴△ACB≌△CDE,∴AC=CD.
在Rt△ABC 中,∠B=90°,∠ACB=30°,AB=3.5,∴AC=2AB=7,∴CD=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:
 ,求大楼AB的高度是多少?(精确到0.1米,参考数据:
,求大楼AB的高度是多少?(精确到0.1米,参考数据: 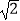 ≈1.41,
≈1.41,  ≈1.73,
≈1.73,  ≈2.45)
≈2.45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,连结CD,某抛物线y=ax2+bx+c(a≠0)经过点D、点E(1,1).

(1)若该抛物线过原点O,则a=;
(2)若点Q在抛物线上,且满足∠QOB与∠BCD互余,要使得符合条件的Q点的个数是4个,则a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人(两人走的路线相同)?试求解这个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大石桥市政府为了落实“暖冬惠民工程”,计划对城区内某小区的部分老旧房屋及供暖管道和部分路段的人行地砖、绿化带等公共设施进行全面更新改造。该工程乙队单独完成所需天数是甲队单独完成所需天数的1.5倍 , 若甲队先做10天,剩下两队合作30天完成。
(1)甲乙两个队单独完成此项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙对每天的施工费用为5.6万元,工程施工的预算费用为500万元,为了缩短工期并高效完成工程,拟预算的费用是否够用?若不够用,需追加预算多少万元?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
相关试题

