【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

参考答案:
【答案】(1)30°;(2)4.
【解析】
试题(1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
试题解析:(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=2,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
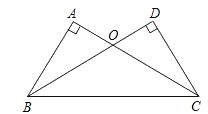
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南宁市金陵镇三联村无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
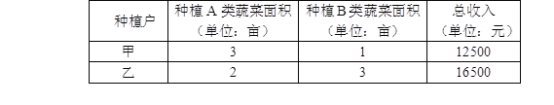
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
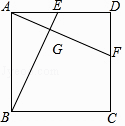
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第100个图中正方形和等边三角形的个数之和是( )

A. 900 B. 903 C. 906 D. 807
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,添加下列条件,还不能使△ABC≌△CDA成立的是( )

A. AD=BC B. ∠BAC=∠ACD C. AB∥DC D. AB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAD的度数为( )
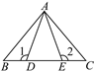
A. 50° B. 60° C. 70° D. 110°
相关试题

