Question

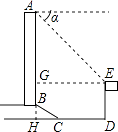
【题目】如图所示，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i=1： ，求大楼AB的高度是多少？（精确到0.1米，参考数据： ≈1.41， ≈1.73， ≈2.45）

Answer 1

【答案】解：延长AB交DC于H，作EG⊥AB于G，如图所示：

则GH=DE=15米，EG=DH，

∵梯坎坡度i=1： ，

∴BH：CH=1： ，

设BH=x米，则CH= x米，

在Rt△BCH中，BC=12米，

由勾股定理得：x2+（ x）2=122，

解得：x=6，

∴BH=6米，CH=6 米，

∴BG=GH﹣BH=15﹣6=9（米），EG=DH=CH+CD=6 +20（米），

∵∠α=45°，

∴∠EAG=90°﹣45°=45°，

∴△AEG是等腰直角三角形，

∴AG=EG=6 +20（米），

∴AB=AG+BG=6 +20+9≈39.4（米）．

故大楼AB的高度大约是39.4米．

【解析】延长AB交DC于H，作EG⊥AB于G，则GH=DE=15米，EG=DH，设BH=x米，则CH= x米，在Rt△BCH中，BC=12米，由勾股定理得出方程，解方程求出BH=6米，CH=6 米，得出BG、EG的长度，证明△AEG是等腰直角三角形，得出AG=EG=6 +20（米），即可得出大楼AB的高度．
【考点精析】根据题目的已知条件，利用关于仰角俯角问题的相关知识可以得到问题的答案，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．