搜索
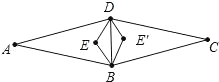
【题目】在菱形ABCD中，∠A=30°，在同一平面内，以对角线BD为底边作顶角为120°的等腰三角形BDE，则∠EBC的度数为 ．
参考答案：
【答案】105°或45°
【解析】
试题分析：如图当点E在BD右侧时，求出∠EBD，∠DBC即可解决问题，当点E在BD左侧时，求出∠DBE′即可解决问题．如图，∵四边形ABCD是菱形，∴AB=AD=BC=CD，∠A=∠C=30°，∠ABC=∠ADC=150°，
∴∠DBA=∠DBC=75°，∵ED=EB，∠DEB=120°，∴∠EBD=∠EDB=30°，∴∠EBC=∠EBD+∠DBC=105°，
当点E′在BD左侧时，∵∠DBE′=30°，∴∠E′BC=∠DBC﹣∠DBE′=45°，∴∠EBC=105°或45°，
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读并解决其后的问题：我们将四个有理数
、
、
、
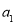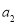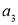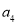写成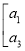
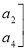的形式，称它为由有理数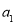、、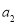、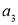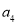组成的二阶矩阵，称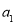、、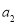、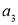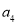为构成这个矩阵的元素，如由有理数
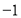、2、3、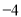
组成的二阶矩阵是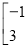
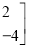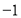，、2、3、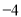是这个矩阵的元素，当且仅当两个矩阵相同位置上的元素相等时，我们称这两个二阶矩阵相等，下面是两个二阶矩阵的加法运算过程：①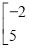
+
=
=
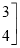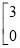
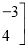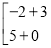
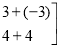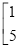
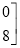，②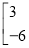
+
=
=
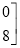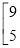
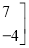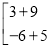
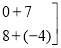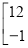
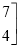，（1）通过观察上述例子中矩阵加法运算的规律，可归纳得二阶矩阵的加法运算法则是：两个二阶矩阵相加， .
（2）①计算：
+
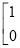
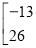
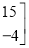；②若
+
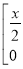
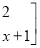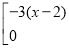
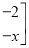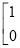
= ，求
的值；（3）若记A=
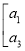
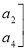，B=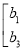
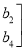，试依据二阶矩阵的加法法则说明A+B=B+A成立 -
科目： 来源： 题型：
查看答案和解析>>【题目】为了丰富课外活动，某校将购买一些乒乓球拍和乒乓球，某商场销售一种乒乓球拍和乒乓球，乒乓球拍每副定价80元，乒乓球每盒定价20元，“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：买一副乒乓球拍送一盒乒乓球；
方案二：乒乓球拍和乒乓球都按定价的90%付款．
某校要到该商场购买乒乓球拍20副，乒乓球
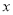盒(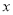>20且为整数)．（1）若按方案一购买，需付款 元(用含
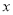的整式表示，要化简)； 若按方案二购买，需付款 元(用含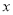的整式表示，要化简).（2）若
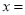30，通过计算说明此时按哪种方案购买较为合算？（3）当
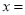30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝6，AC＝4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N，则△AMN的周长为（ ）
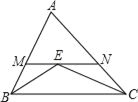
A. 12B. 10C. 8D. 不确定
-
科目： 来源： 题型：
查看答案和解析>>【题目】读句画图并完成计算：如图，直线AB与直线CD交于点C ,
(1)过点P作PQ∥CD，交AB于点Q；
(2)过P作PR⊥CD于点R；
(3)若∠DCB=150，求∠PQC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在等边△ABC中取点P，使得PA，PB，PC的长分别为3，4，5，将线段AP以点A为旋转中心顺时针旋转60°得到线段AD，连接BD，下列结论：
①△ABD可以由△APC绕点A顺时针旋转60°得到；②点P与点D的距离为3；③∠APB＝150°；
④S△APC+S△APB＝
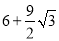，其中正确的结论有（ ）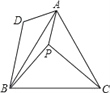
A. ①②④B. ①③④C. ①②③D. ②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y1＝k1x+2与反比例函数y2＝
的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C．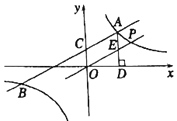
（1）k1＝ ，k2＝ ；
（2）根据函数图象可知，当y1＞y2时，x的取值范围是 ；
（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE＝3：1时，求直线OP的解析式．
相关试题
